• Βασικά σχήματα - Τρίγωνα - Παραλληλόγραμμα
• Εγγεγραμμένα σχήματα - Λόγοι - Ομοιότητα
• Μετρικές σχέσεις
• Εμβαδά
• Κανονικά πολύγωνα - Κύκλος
• Στερεομετρία

• Το Α₂ επί ερωτημάτων, της Ειρήνης Περυσινάκη [Σ+Π]
  Περιγραφή: Η ιδέα αυτού του μαθήματος είναι μάλλον απλή: Δίνεται στους μαθητές μια ημιτελής εκφώνηση άσκησης (λείπουν τα συμπεράσματα) και τους ζητείται σε πρώτη φάση να συμπληρώσουν την εκφώνηση και σε δεύτερη να προσπαθήσουν να λύσουν τα προβλήματα που έθεσαν οι ίδιοι. Αξιοσημείωτη η πλούσια φαντασία των μαθητών και η ικανότητά τους να διατυπώνουν εικασίες που ίσως δεν μπορούν να αποδείξουν. Ο πειραματισμός αυτός διήρκησε 4 διδακτικές ώρες περίπου, τον Νοέμβριο του 2009.



---



• Θεωρήματα ΙΙΙ και IV της παρ. 3.6, ένα σχέδιο μαθήματος της Ειρήνης Περυσινάκη [Σ+Π]
  Περιγραφή: Τα θεωρήματα ΙΙΙ και IV της παραγράφου 3.6 αναφέρονται στη σχέση χορδών και αποστημάτων (ίσες χορδές ενός κύκλου έχουν ίσα αποστήματα και αντίστροφα) και στην ιδιότητα των σημείων της διχοτόμου γωνίας να ισαπέχουν από τις πλευρές της γωνίας. Στο παρόν σχέδιο μαθήματος γίνεται ο συνδυασμός αυτών των θεωρημάτων. Η διδακτική πρόταση έχει εφαρμοστεί αρκετές φορές.



---



• Η τριχοτόμηση της γωνίας, της Ειρήνης Περυσινάκη [Σ+Π]
  Περιγραφή: Δύο ασκήσεις του σχολικού βιβλίου, η αποδεικτική άσκηση 2 σελ. 63 (Κεφ. 3) και η άσκηση εμπέδωσης 5 σελ. 87 (Κεφ. 4), μπορούν να ειδωθούν υπό το πρίσμα της διερεύνησης του θέματος της τριχοτόμησης γωνίας. Γιατί να είναι αδύνατη με κανόνα και διαβήτη; Υπάρχουν άλλα μέσα για να επιτευχθεί; Οι μαθητές, μαθαίνουν για την μέθοδο νεύσης του Αρχιμήδη, για τον τριχοτόμο tomahauk, για την τριχοτόμηση με μεθόδους χαρτοδιπλωτικής. Το μάθημα εφαρμόστηκε στις 17/02/10 και 02/02/11.



---



• Τα κέντρα τριγώνου - Ευθεία Euler, της Ειρήνης Περυσινάκη [Σ+Π]
  Περιγραφή: Οι μαθητές διερευνούν την σχετική θέση του ορθόκεντρου, του βαρύκεντρου και του περίκεντρου τριγώνου, για να διαπιστώσουν πως πάντα αυτά είναι συνευθειακά (ευθεία Euler). Το μάθημα αυτό εφαρμόστηκε στις 07/04/09.
  Λογισμικό: GeoGebra 3.0, λογισμικό δυναμικής Γεωμετρίας και επεξεργασίας Αλγεβρικών Συστημάτων (CAS - Computer Algebra Systems)



---



• Δύο ισοσκελή και ένα ορθογώνιο τρίγωνο, της Ειρήνης Περυσινάκη [Σ+Π]
  Περιγραφή: Οι μαθητές ασχολούνται με ένα ερώτημα τύπου "πάζλ". Αν τους δωθούν δύο ισοσκελή τρίγωνα, τότε ποια σχήματα μπορούν να κατασκευάσουν με αυτά, όταν τα ενώσουν χωρίς επικαλύψεις; Ή και αντίστροφα: Αν τους δοθεί ένα γεωμετρικό σχήμα, είναι δυνατόν να διαιρεθεί σε δύο ισοσκελή τρίγωνα; Ειδικότερα, τι ισχύει για ένα τυχαίο τρίγωνο; Πότε διαιρείται σε δύο ισοσκελή;
  Το αποτέλεσμα μη αναμενόμενο: Κάθε ορθογώνιο τρίγωνο διαιρείται σε δύο ισοσκελή, άπειρα σκαληνά τρίγωνα διαιρούνται σε δύο ισοσκελή, ενώ μόνο δύο ισοσκελή τρίγωνα διαιρούνται σε δύο ισοσκελή.
  Η πρόταση διδασκαλίας αποτελεί μια άλλη οπτική στο θεώρημα διαμέσου ορθογωνίου τριγώνου που αντιστοιχεί στην υποτείνουσα.
  Λογισμικό: The Geometer's Sketchpad V4, λογισμικό δυναμικής Γεωμετρίας



---



• Οι καταπληκτικές ιδέες του Β₃ για το ισοσκελές τραπέζιο, της Ειρήνης Περυσινάκη [Σ+Π]
  Περιγραφή: Στις 3/10/12, οι μαθητές του Β₃ πρότειναν πολύ ενδιαφέροντες τρόπους για την κατασκευή ενός ισοσκελούς τραπεζίου. Κάθε πρόταση ελέγχθηκε με το λογισμικό GeoGebra στον διαδραστικό πίνακα που διαθέτει η αίθουσα. Σε περίπτωση λάθους, έγιναν οι απαραίτητες τροποποιήσεις.
  Λογισμικό: GeoGebra 4.2, λογισμικό δυναμικής Γεωμετρίας και επεξεργασίας Αλγεβρικών Συστημάτων (CAS - Computer Algebra Systems)

Επιστροφή στην αρχή
Επιστροφή στην αρχή της ενότητας

• Σημείο Fermat και Τέχνη, της Αθανασίας Σούφαρη
  Περιγραφή: Με αφορμή έναν πίνακα του Suman Vaze, η συγγραφέας ετοίμασε μια διαδραστική παρουσίαση GeoGebra που παρουσιάζει τις ιδιότητες και τον τρόπο κατασκευής του σημείου Fermat ενός τριγώνου. Η κύρια ιδιότητά του είναι ότι το άθροισμα των αποστάσεών του από τις κορυφές του τριγώνου είναι ελάχιστο.
  Λογισμικό: GeoGebra 5.0, λογισμικό δυναμικής Γεωμετρίας και επεξεργασίας Αλγεβρικών Συστημάτων (CAS - Computer Algebra Systems)



---



• Η εκτέλεση ενός γεωμετρικού «μαγικού» βήμα-βήμα, του Λαμπράκη Μανώλη
  Περιγραφή: Πώς μπορούμε να εγγράψουμε ένα ισόπλευρο τρίγωνο σε ένα ορθογώνιο τρίγωνο; Μήπως η κατασκευή κρύβει κάτι το μαγικό, έναν γεωμετρικό μετασχηματισμό; Διαβάστε το άρθρο για να το ανακαλύψετε.



---



• Προβληματισμός για τη διδασκαλία των θεωρημάτων διχοτόμων τριγώνου στο Λύκειο, των καθηγητών του Πειραματικού Λυκείου Ηρακλείου
  Περιγραφή: Τα τελευταία χρόνια τα θεωρήματα διχοτόμων διδάσκονται "εν τάχει" στην Β' Λυκείου, καθώς αποτελούν ύλη της Α' Λυκείου που δεν ολοκληρώθηκε και συνεπώς πρέπει να διδαχθεί κατά τις πρώτες μέρες του έτους. Αυτό υποβαθμίζει τα θεωρήματα. Καταθέτουμε λοιπόν μια πρόταση ανάδειξής τους σε άλλο σημείο της διδακτέας ύλης της Β' Λυκείου.

Επιστροφή στην αρχή
Επιστροφή στην αρχή της ενότητας

• Πυθαγόρειο Θεώρημα και Πυθαγόρειες Τριάδες, της Ειρήνης Περυσινάκη [Σ+Π]
  Περιγραφή: Παρουσιάζονται οι διάλογοι στο μάθημα της 9/11/11 στο Β2, όπου οι μαθητές γνώρισαν τις κλασσικές αποδείξεις του Πυθαγορείου Θεωρήματος από τον Πυθαγόρα και τον Ευκλείδη, καθώς και ένα γεωμετρικό επιχείρημα για τον εντοπισμό πρωταρχικών Πυθαγόρειων τριάδων. Το ίδιο μάθημα εφαρμόστηκε και στα τμήματα Β1 (4/11/11) και στο Β3 (9/11/11).
  Λογισμικό: GeoGebra 3.2, λογισμικό δυναμικής Γεωμετρίας και επεξεργασίας Αλγεβρικών Συστημάτων (CAS - Computer Algebra Systems)



---



• Γεωμετρικές ακροβασίες, του Λαμπράκη Μανώλη, Φυσικός στο Πρότυπο ΠΛΗ [Σ]
  Περιγραφή: Δύο ωραία προβλήματα μεγιστοποίησης-ελαχιστοποίησης, το ένα δυϊκό του άλλου, αξιοποιούν τη γνωστή ιδιότητα του ύψους που αντιστοιχεί στην υποτείνουσα ορθογωνίου τριγώνου, να έχει τετράγωνο ίσο με το γινόμενο των προβολών των κάθετων πλευρών στην υποτείνουσα.
  Στο πρώτο πρόβλημα ζητείται να βρεθεί η μέγιστη τιμή του γινομένου δύο θετικών αριθμών που έχουν ένα σταθερό άθροισμα, ενώ στο δεύτερο (ως δυϊκό του πρώτου) ζητείται να βρεθεί η ελάχιστη τιμή του αθροίσματος δύο θετικών αριθμών με σταθερό γινόμενο. Στις δύο γεωμετρικές προσεγγίσεις, διαφαίνεται η δυϊκή σχέση ευθείας-κύκλου. Στο τέλος, ο συγγραφέας δίνει ένα ωραίο γύμνασμα για τους αναγνώστες του.



---



• Μέγιστα και ελάχιστα της Β’ Λυκείου με μαθηματικά της Β’ Γυμνασίου, του Λαμπράκη Μανώλη, Φυσικός στο Πρότυπο ΠΛΗ [Σ]
  Περιγραφή:Μια αλγεβρική ανισότητα με πρωτότυπη γεωμετρική προσέγγιση, όπου αξιοποιούνται το Πυθαγόρειο θεώρημα και η ανισοτική σχέση κάθετων και πλάγιων τμημάτων.
  Σημείωση: Το άρθρο αποτελεί αναδημοσίευση από την εκπαιδευτική πύλη "Υλικό Φυσικής-Χημείας".



---



• Ένα πρόβλημα Γεωμετρίας με έμφαση στην ακολουθούμενη πορεία, του Λαμπράκη Μανώλη, Φυσικός στο Πρότυπο ΠΛΗ [Σ]
  Περιγραφή: Ένα ωραίο πρόβλημα στο Πυθαγόρειο Θεώρημα όπου αξιοποιείται η σχέση του ύψους που αντιστοιχεί στην υποτείνουσα ενός ορθογωνίου τριγώνου με τις κάθετες πλευρές του.
  Σημείωση:Το άρθρο αποτελεί αναδημοσίευση από την εκπαιδευτική πύλη "Υλικό Φυσικής-Χημείας".

Επιστροφή στην αρχή
Επιστροφή στην αρχή της ενότητας

• Το εμβαδόν ορθογωνίου και πλάγιου παραλληλογράμμου, της Ειρήνης Περυσινάκη [Σ+Π]
  Περιγραφή: Οι μαθητές, χωρισμένοι σε ομάδες και καθοδηγούμενοι από φύλλο εργασίας, εμπλέκονται σε δραστηριότητες τύπου παζλ ή καλύτερα "κόψε-ράψε". Στόχος να εντοπίσουν για κάθε ορθογώνιο παραλληλόγραμμο τρία τετράγωνα που καθορίζουν το εμβαδόν του ορθογωνίου. Μέσα από την διαδικασία διερεύνησης, αναδεικνύεται η αξιωματική θεμελίωση της έννοιας του εμβαδού. Το μάθημα πραγματοποιήθηκε στα πλαίσια δειγματικής διδασκαλίας στο Εργαστήριο Μαθηματικών, στις 03/02/10.



---



• Το θεώρημα του Pick, της Ειρήνης Περυσινάκη [Σ+Π]
  Περιγραφή: Με αφορμή τον υπολογισμό του εμβαδού του παρακάτω τριγώνου, ξεκινάει μια κουβέντα στην τάξη για το θεώρημα του Pick το οποίο διατυπώνει το εξής: "Αν ένα απλό πολύγωνο έχει κορυφές σημεία ενός τετραγωνικού πλέγματος με τετράγωνα πλευράς 1, τότε το εμβαδόν του υπολογίζεται από τον εξής τύπο: Ε=Κ_εσ + Κ_περ/2 - 1, όπου Κ_εσ= κουκίδες στο εσωτερικό του πολυγώνου και Κ_περ= κουκίδες στην περίμετρο του πολυγώνου." To μάθημα αυτό πραγματοποιήθηκε στις 18/02/10, 31/01/11, 08/02/11 και 04/03/11.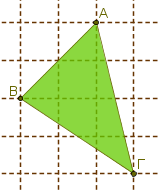 Μια απόδειξη του θεωρήματος στα ελληνικά είναι εδώ, ενώ στα αγγλικά υπάρχουν και διαδραστικές εφαρμογές, όπως αυτή από το "Cut the knot" και αυτή από το "National Grid for Learning", την οποία μπορείτε να κατεβάσετε στον σκληρό σας από εδώ.



---



• Transformer! Ένα παράδειγμα ισοδύναμων σχημάτων - Μια σπαζοκεφαλιά του Dudney, της Ειρήνης Περυσινάκη [Σ+Π]
  Περιγραφή: Ένα από τα πολύ όμορφα παζλ του εργαστηρίου, που προκαλεί το ερέθισμα για συζήτηση στα ισοδύναμα σχήματα, είναι το πώς, τα ίδια τέσσερα τετράπλευρα μπορούν να ενωθούν με δύο διαφορετικές διατάξεις, φτιάχντας πρώτα ένα τετράγωνο και έπειτα ένα τρίγωνο. Αφού οι μαθητές ασχοληθούν με αυτό το ελκυστικό παζλ, ακολουθεί η προβολή ενός απίθανου "χορού των σχημάτων", ακριβώς όπως το εμπνεύστηκε ο Dudney. Για περισσότερη ενασχόληση τους δίνεται και ένα φύλλο εργασίας. Το μάθημα πραγματοποιήθηκε στις 20/02/09.



---



• Το ισοπεριμετρικό πρόβλημα και ο μύθος της Διδούς, του Δημήτρη Καλυκάκη [Σ+Π]
  Περιγραφή: Το ισοπεριμετρικό πρόβλημα είναι, σύμφωνα με τους ειδικούς, το αρχαιότερο ίσως πρόβλημα μεγιστοποίησης, που με απλά λόγια λέει το εξής: Από όλες τις καμπύλες του επιπέδου που έχουν το ίδιο μήκος, αυτή που περικλείει χωρίο με το μέγιστο δυνατό εμβαδόν είναι ο κύκλος. Η παράδοση συνδέει το πρόβλημα αυτό με το μύθο της Διδούς, της βασίλισσας της Καρχηδόνας, που τοποθετείται περίπου στον 9ο π.Χ. αιώνα, και που ο Βιργίλιος διασώζει στο επικό του ποίημα την Αινειάδα. Εδώ βρίσκεται μια διδακτική πρόταση προσαρμοσμένη για μαθητές Λυκείου.



---



• Φυλλάδιο ασκήσεων στη σύγκριση εμβαδών ομοίων σχημάτων, της Ειρήνης Περυσινάκη [Σ+Π]
  Περιγραφή: Πρόκειται για ένα φυλλάδιο ασκήσεων, κατά κανόνα απλών, στα θεωρήματα σύγκρισης εμβαδών ομοίων πολυγώνων. Στην προ-τελευταία άσκηση υπάρχει ένα είδος γενίκευσης, όπου ζητείται το εμβαδόν τριγώνου, εάν είναι γνωστό το εμβαδόν ενός πλάγιου παραλληλογράμμου. Στην τελευταία άσκηση ζητείται η κατασκευή ενός τραπεζίου, γνωρίζοντας τα εμβαδά των τριγώνων που σχηματίζουν οι κορυφές του. Το φυλλάδιο αυτό συζητήθηκε στην τάξη, στις 26/03/10.

Επιστροφή στην αρχή
Επιστροφή στην αρχή της ενότητας

• Μωσαϊκό κανονικών πολυγώνων, της Ειρήνης Περυσινάκη [Σ+Π]
  Περιγραφή: Στις 31 Ιανουαρίου 2017, οι μαθητές του Β1 "μεταμόρφωσαν" κυκλικά χαρτιά σε εντυπωσιακές τριγωνικές ψηφίδες και κατασκεύασαν ένα μοναδικό μωσαϊκό. Η κατασκευή κάθε ψηφίδας απαιτεί την έξυπνη εφαρμογή των κανόνων της χαρτοδιπλωτικής για την εγγραφή ισόπλευρου τριγώνου σε κύκλο.



---



• Κανονικά πολύγωνα και γρίφοι χαρτοδιπλωτικής, της Ειρήνης Περυσινάκη [Σ+Π]
  Περιγραφή: Δίνονται στους μαθητές κυκλικά χαρτιά (π.χ. κόλλες περιτυλίγματος όπου σχεδιάστηκαν με CD κύκλοι που κόπηκαν) και ζητείται από αυτούς, να τα διπλώσουν κατάλληλα, ώστε να σχηματιστούν εγγεγραμμένα τετράγωνα, κανονικά εξάγωνα και ισόπλευρα τρίγωνα. Ο "γρίφος" αυτός δεν είναι καθόλου απλός και απαιτεί μαθηματικές τεχνικές όμοιες με εκείνες που εφαρμόζονται με κανόνα και διαβήτη. Το μάθημα αυτό εφαρμόστηκε στις 03/04/2009.



---



• Προσεγγίζοντας τον κύκλο με κανονικά πολύγωνα, της Ειρήνης Περυσινάκη [Σ+Π]
  Περιγραφή: Δύο πειραματισμοί με το λογισμικό GeoGebra. Με τον πρώτο, οι μαθητές κινούν δρομέα και παρατηρούν ότι όσο μεγαλύτερο είναι το πλήθος των πλευρών ενός εγγεγραμμένου κανονικού πολυγώνου σε έναν κύκλο, τόσο περισσότερο το μήκος του πολυγώνου προσεγγίζει το μήκος του κύκλου. Ο δεύτερος πειραματισμός είναι παρόμοιος: ο δρομέας μεταβάλλει συγχρόνως το πλήθος των πλευρών εγγεγραμμένου κανονικού πολυγώνου και του αντίστοιχου περιγεγραμμένου στον ίδιο κύκλο πολυγώνου, με σημεία επαφής τις κορυφές του εγγεγραμμένου. Έτσι, με μια ιδιότητα "σάντουιτς", προσεγγίζεται το εμβαδόν του κυκλικού δίσκου. Το μάθημα αυτό πραγματοποιήθηκε στις 27/03/09. Στο ίδιο πνεύμα είναι και οι δραστηριότητες εδώ.
  Λογισμικό: GeoGebra 3.2, λογισμικό δυναμικής Γεωμετρίας και επεξεργασίας Αλγεβρικών Συστημάτων (CAS - Computer Algebra Systems)



---



• Κατασκευή κανονικών πολυγώνων στον "χελωνόκοσμο", της Ειρήνης Περυσινάκη [Σ+Π]
  Περιγραφή: Ο σύνδεσμος παραπέμπει στο εισαγωγικό μάθημα γνωριμίας με τον μικρόκοσμο "χελονόκοσμο", που πραγματοποιήθηκε στο Εργαστήριο Πληροφορικής, στις 22/04/10. Η τελευταία δραστηριότητα είναι η κατασκευή τετραγώνου, ισόπλευρου τριγώνου, κανονικού εξαγώνου. Οι μαθητές, εύκολα γενίκευσαν την διαδικασία για την κατασκευή οποιουδήποτε κανονικού πολυγώνου. Η κατασκευή με τον Χελωνόκοσμο αναδεικνύει ιδιότητες των κανονικών πολυγώνων, όπως ότι έχουν περιστροφική συμμετρία και ότι "οριακά" γίνονται κύκλοι. Αυτό δηλώνει και την ύπαρξη του κέντρου του πολυγώνου, παρόλο που η χελώνα του χελωνόκοσμου το "αγνοεί" κατά την κίνησή της. Ας σημειωθεί ακόμα ότι οι μαθητές επέκτειναν την έννοια του πολυγώνου και σε αστεροειδή πολύγωνα.
  Λογισμικό: Ο μικρόκοσμος "Χελωνόκοσμος" του ελεύθερου λογισμικού "Αβάκιο", του Εργαστηρίου Εκπαιδευτικής Τεχνολογίας.

Επιστροφή στην αρχή
Επιστροφή στην αρχή της ενότητας

• Στερεο-ανακαλύψεις, της Ειρήνης Περυσινάκη [Σ+Π]
  Περιγραφή: Οι μαθητές συρράπτουν τετράγωνα και τρίγωνα από χαρτόνι με στόχο να δημιουργήσουν συγκεκριμένα πολύπλοκα στερεά. Πρώτα όμως, θα πρέπει να κατανοήσουν την δομή αυτών των στερεών. Τον μάθημα πραγματοποιήθηκε τον Μάρτιο του 2011 (δείτε το εδώ).

Επιστροφή στην αρχή
Επιστροφή στην αρχή της ενότητας