Το τμήμα μου Β1, διπλώνοντας κυκλικά χαρτιά

Διαιρώντας τον κύκλο σε τεταρτημόρια...

...και παίρνοντας το εγγεγραμμένο τετράγωνο.

Η άλλη όψη του τετραγώνου

Μερικά τετράγωνα ακόμη

8 τομείς αντί για 6
Το κανονικό εξάγωνο είναι πραγματικά ζόρικο!

Αλλά το οκτάγωνο δίνει γουστόζικα τετράγωνα.
Μπροστά...

...και πίσω.

Ας σκεφτούμε βαθύτερα για το κανονικό εξάγωνο!

Χρειαζόμαστε περισσότερα κυκλικά χαρτιά

Εύρηκα!
Ξεκινάμε με τον κύκλο διαιρεμένο σε τέταρτα,

φέρνουμε τα άκρα μιας διαμέτρου στο κέντρο
για να λάβουμε 4 επιπλέον σημεία στον κύκλο.

Διπλώνουμε τις έξι χορδές για το εξάγωνο

Γυρνάμε ανάποδα και διπλώνουμε τις πλευρές του ισόπλευρου τριγώνου..

Και το πλακάκι μας είναι έτοιμο!

Να κι άλλο ένα!

Ας κατασκευάσουμε όλοι μερικά πλακάκια για το μωσαϊκό

τώρα έχουμε αρκετά!

Αυτό το μωσαϊκό φαίνεται ωραίο.

Αλλά αυξήθηκαν τα πλακάκια
και αναγκαζόμαστε να αλλάξουμε σχέδιο.

Ώρα να κολλήσουμε τα πλακάκια.

Πολύ προσεκτικά, να τακτοποιηθούν όλα.

Δείτε! Ένα τέλειο μωσαϊκό!

Κρεμάστε το στην κρεμάστρα.

Τα επιπλέον πλακάκια θα πάνε στους τοίχους...

...ή στον μαυροπίνακα για διακόσμηση.

Το μωσαϊκό

με λουλουδένιες μπάλες σε μία έκθεση

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28

Στη Γεωμετρία της Β’ Λυκείου οι μαθητές γνωρίζουν τα κανονικά πολύγωνα και πώς να τα εγγράφουν σε έναν κύκλο. Η ιδέα είναι ότι εφόσον ο κύκλος διαιρεθεί σε «ν» ίσα τόξα, τότε, οι αντίστοιχες χορδές σχηματίζουν ένα κανονικό ν-γωνο (σχήμα 1). Η κατασκευή δεν είναι πάντα εφικτή με κανόνα και διαβήτη.

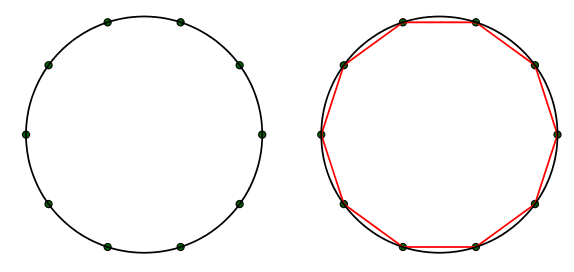
Σχήμα 1: Γενική μέθοδος για την εγγραφή κανονικού πολυγώνου σε κύκλο.

Στις 31 Ιανουαρίου 2017, ο προγραμματισμός μου ήταν να διδάξω τους μαθητές μου του τμήματος Β1 πώς να χρησιμοποιούν τον κανόνα και τον διαβήτη για να εγγράφουν σε δοσμένο κύκλο τα βασικά κανονικά πολύγωνα, δηλαδή το τετράγωνο, το κανονικό εξάγωνο και το ισόπλευρο τρίγωνο. Αντί γι’ αυτό, αποφάσισα να χρησιμοποιήσω κυκλικά χαρτιά και τους κανόνες χαρτοδιπλωτικής σε μια εργαστηριακή δραστηριότητα που θα κατέληγε σε ένα τελικό προϊόν, ένα μωσαϊκό.

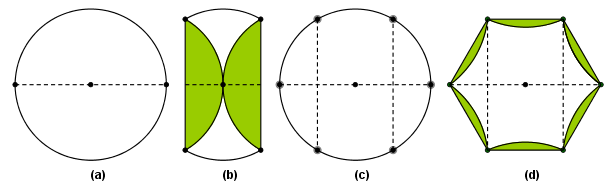
Οι κανόνες της χαρτοδιπλωτικής έχουν μια ακρίβεια συγκρίσιμη με εκείνους του "κανόνα και του διαβήτη". Για παράδειγμα, εάν κάποιος θέλει να κατασκευάσει μια διάμετρο ενός κυκλικού χαρτιού, δεν έχει παρά να διπλώσει τον κύκο στη μέση, έτσι ώστε τα δύο μισά να συμπέσουν (σχήμα 2). Χωρίς αμφιβολία, η δίπλωση που σχηματίστηκε είναι διάμετρος, καθώς αποτελεί άξονα συμμετρίας του κύκλου. Κατά τον ίδιο τρόπο, κάποιος μπορεί να κατασκευάσει με συμμετρικές διπλώσεις τη διαγώνιο ενός τετραγώνου, τη μεσοκάθετο ενός τμήματος κ.α.

Σχήμα 2: Μια ακριβής κατασκευή με χαρτοδιπλωτική μιας διαμέτρου ενός κύκλου.

Η πρώτη άσκηση ήταν η εγγραφή ενός τετραγώνου. Αυτό ήταν εύκολο για τους μαθητές μου και πραγματοποιήθηκε σε δευτερόλεπτα: δίπλωσαν το κυκλικό χαρτί στη μέση και πάλι στη μέση και όταν ξεδίπλωσαν, είχαν σχηματιστεί δύο κάθετες διάμετροι που διαιρούσαν τον κύκλο σε τέταρτα (σχήμα 3). Η δίπλωση των χορδών ολοκλήρωνε την άσκηση.

Σχήμα 3: Η κατασκευή του εγγεγραμμένου τετραγώνου.

Η δεύτερη άσκηση ήταν πραγματικά απαιτητική. Πώς ήταν δυνατόν να εγράψει κάποιος –με ακρίβεια- το κανονικό εξάγωνο; Διαδοχικές διπλώσεις στη μέση, που ήταν το πρώτο πράγμα που δοκίμασαν οι μαθητές μου, οδηγούσαν σε κανονικό οκτάγωνο (σχήμα 4).

Σχήμα 4: Διαδοχικές διπλώσεις στο ήμισυ διαιρούν τον κύκλο σε 8 τομείς αντί για 6.

Χρειάστηκαν λίγο χρόνο μέχρι να ανακαλύψουν το κόλπο: έχοντας μια διάμετρο και το μέσο της ως το κέντρο του κύκλου, το επόμενο βήμα είναι να σχηματίσουν τις μεσοκαθέτους των δύο μισών της διαμέτρου (ακτίνες), φέροντας τα άκρα της στο κέντρο (σχήμα 5). Τα τέσσερα σημεία του κύκλου που ορίζονται έτσι, μαζί με τα άκρα της διαμέτρου, αποτελούν τις κορυφές του κανονικού εξαγώνου. Θα αφήσουμε στον αναγνώστη την άσκηση να κατανοήσει τα μαθηματικά που κρύβονται πίσω από την κατασκευή.

Εάν από τις έξι κορυφές του κανονικού εξαγώνου πάρουμε κάθε δεύτερο σημείο, θα πάρουμε τις τρεις κορυφές του ισόπλευρου τριγώνου (σχήμα 6).

Σχήμα 5: Εγγράφοντας ένα κανονικό πολύγωνο σε κύκλο, με τους κανόνες της χαρτοδιπλωτικής.

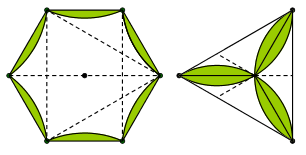
Σχήμα 6: Από το κανονικό εξάγωνο στο ισόπλευρο τρίγωνο.

Το καταπληκτικό κόλπο διαδόθηκε σε όλους και η Τάξη ξεκίνησε να παράγει όλο και περισσότερα από τα εντυπωσιακά ροζ-πράσινα τριγωνικά πλακάκια. Σημειώθηκε τόσο μεγάλη παραγωγή που δεν χρησιμοποιήθηκαν όλα τα πλακάκια για το μωσαϊκό. Τίποτα όμως δεν πήγε χαμένο. Τα επιπλέον πλακάκια διακόσμησαν τον μαυροπίνακα, την πόρτα και άλλα σημεία της αίθουσας.

• Κανονικά πολύγωνα και γρίφοι χαρτοδιπλωτικής της Ειρήνης Περυσινάκη
• Από τον κύκλο στα κανονικά πολύγωνα με χαρτοδιπλωτική, της Ειρήνης Περυσινάκη, δημοσιευμένο στον "Ευκλείδη Α", Τεύχος 103 (2017), 9-12