Μείναμε λίγο πίσω με το περυσινό Α₄ στη Γεωμετρία και ως Β₃ απλώς συζητάω μαζί τους όσα θεωρώ σημαντικά, για να πάμε παρακάτω.

Ίσως να μην είναι και τόσο "σημαντικό" το ισοσκελές τραπέζιο, όμως κανείς μπορεί να θέσει αρκετά ενδιαφέροντα ερωτήματα που ετοιμάζουν το έδαφος για τις επόμενες γεωμετρικές ιδέες, όπως ομοιότητα, εγγεγραμμένη γωνιά κ.α.

Στην πρώτη μου ερώτηση, για το ποιο νομίζουν ότι είναι το ισοσκελές τραπέζιο απάντησαν άμεσα και σωστά: αυτό που έχει τις μη-παράλληλες πλευρές του ίσες. Εύκολα εντόπισαν και τις ιδιότητές του: οι προσκείμενες γωνίες σε κάθε βάση του είναι ίσες και οι διαγώνιοί του είναι πάλι ίσες.

Και τώρα, το ερώτημα που θα αναδείκνυε τα κριτήρια για το ισοσκελές τραπέζιο:
Πώς θα μπορούσαμε να κατασκευάσουμε γεωμετρικά ένα ισοσκελές τραπέζιο;
Κάθε πρόταση θα έπρεπε να περάσει από τρία στάδια:

1. Ο μαθητής παρουσιάζει την ιδέα της κατασκευής του
2. Μεταφέρουμε την ιδέα βήμα-βήμα στο λογισμικό GeoGebra και διαπιστώνουμε αν είναι κατασκευάσιμη. Εδώ γίνεται η χρήση του διαδραστικού πίνακα της αίθουσας διδασκαλίας.
3. Ελέγχουμε αποδεικτικά εάν το σχήμα που κατασκευάσαμε είναι ισοσκελές τραπέζιο

Σημεία ανάπτυξης

• Η ιδέα του Αντώνη
• Η ιδέα της Βαλέριας
• Μια άσκηση γεννιέται
• Η ιδέα του Δημήτρη και όχι μόνο
• Η άσκηση για το σπίτι
• Συμπεράσματα

Πρώτος ζήτησε τον λόγο ο Αντώνης και έκανε την εξής πρόταση: Ας πάρουμε ένα τμήμα ΑΒ, την μεσοκάθετό του ε και ένα δεύτερο τμήμα ΓΔ που να έχει και αυτό ως μεσοκάθετο την ε. Τότε, το ΑΒΓΔ είναι ισοσκελές τραπέζιο.

Η ιδέα φαινόταν σωστή, όμως "σκοντάψαμε" στην κατασκευή με το Geogebra. Αν φτιάχναμε τυχαία το ΓΔ, κανείς δεν μας εξασφάλιζε ότι θα είχε μεσοκάθετο την ε. Γρήγορα όμως, αλλάξαμε στρατηγική: Θα κατασκευάζαμε πρώτα το Γ και μετά το Δ θα ήταν το συμμετρικό του.

Το "κλειδί" λοιπόν στην ιδέα του Αντώνη ήταν η "συμμετρία", καθώς όχι μόνο τα Γ και Δ ήταν συμμετρικά ως προς την ε, αλλά και τα Α και Β. Συνεπώς, και τα τμήματα ΑΔ, ΒΓ ήταν συμμετρικά ως προς την ε, άρα και ίσα. Όσο για την παραλληλία των ΑΒ και ΓΔ έπεται άμεσα καθώς αυτές είναι κάθετες στην ίδια ευθεία ε.

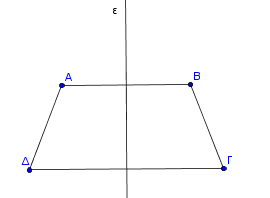
Δείτε την κατασκευή βήμα-βήμα (πατώντας τα βελάκια πλοήγησης στο κάτω μέρος).

Επιστροφή στα σημεία ανάπτυξης

Έπειτα η Βαλέρια πρότεινε το εξής: Να πάρουμε ένα τμήμα ΑΒ και ίσα τμήματα ΑΓ=ΒΔ και να προσπαθήσουμε να τα ενώσουμε στα 2/3 των μηκών τους. Η Βαλέρια εξήγησε ότι δεν ήθελε να ενωθούν στο μέσο για να μην προκύψει παραλληλόγραμμο, κι ότι απλώς ήθελε τον ίδιο λόγο και για τα δύο τμήματα.

Στο παρακάτω σχήμα εμφανίζεται η πρόταση της Βαλέριας με τον λόγο 2/3, δηλαδή ΑΕ=2*ΕΓ και ΒΖ=2*ΖΔ. Όμως καταλάβαμε πως δε μπορούν πάντα να "κολλήσουν" τα σημεία Ε και Ζ σε ένα μοναδικό σημείο (π.χ. όταν το ΑΒ είναι πολύ μεγαλύτερο από τα ΑΓ, ΒΔ).

Επειδή η ιδέα ήταν καλή, είπαμε μήπως μπορούμε να κάνουμε την κατασκευή με διαφορετική σειρά. Έτσι προέκυψε η επόμενη άσκηση.

Δείτε την κατασκευή βήμα-βήμα (πατώντας τα βελάκια πλοήγησης στο κάτω μέρος).

Επιστροφή στα σημεία ανάπτυξης

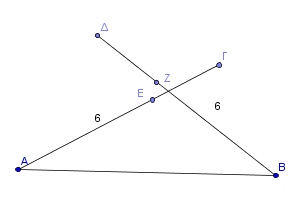
Η τροποποιημένη ιδέα της Βαλέριας ήταν κάπως έτσι: Ας θεωρήσουμε ένα τμήμα ΑΓ και Ε σημείο του με ΑΕ=2*ΕΓ. Από το Ε σχεδιάζουμε μια άλλη ευθεία, έστω ΕΖ, στην οποία παίρνουμε τμήματα ΕΒ=ΕΑ και ΕΔ=ΕΓ εκατέροθεν του ΑΓ, όπως φαίνεται στην επόμενη εικόνα.

Έτσι σχηματίζονται δύο ισοσκελή τρίγωνα, τα ΕΑΒ και ΕΓΔ και δύο ίσα τρίγωνα, τα ΔΕΑ και ΓΕΒ. Συνεπώς, εύκολα δείχνει κανείς την ισότητα των γωνιών ∠ΔΑΒ=∠ΓΒΑ και ∠ΑΔΓ=∠ΒΓΔ, από όπου προκύπτει ότι οι γωνίες ∠ΔΑΒ και ∠ΑΔΓ είναι παραπληρωματικές, άρα και οι ευθείες ΑΒ και ΓΔ παράλληλες.

Δείτε την κατασκευή βήμα-βήμα (πατώντας τα βελάκια πλοήγησης στο κάτω μέρος).

Επιστροφή στα σημεία ανάπτυξης

Τέλος, μίλησε και ο Δημήτρης, ο οποίος πρότεινε κάτι που πολλοί ήταν έτοιμοι να προτείνουν: Να κατασκευάσουμε δύο ισοσκελή τρίγωνα το ένα "επάνω" στο άλλο.

Ένας τρόπος για να γίνει αυτό, είναι να πάρουμε στις πλευρές μιας γωνίας Ο τμήματα ΟΑ=ΟΒ και ΟΔ=ΟΓ, όπως φαίνεται στο επόμενο σχήμα. Προφανώς τότε ΑΔ=ΒΓ και ΑΒ//ΓΔ, καθώς εύκολα διαπιστώνουμε την ισότητα των τεσσάρων γωνιών ∠ΟΑΒ=∠ΟΒΑ=∠ΟΓΔ=∠ΟΔΓ.

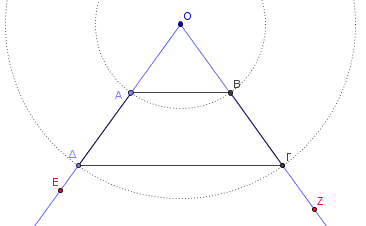
Δείτε την κατασκευή βήμα-βήμα (πατώντας τα βελάκια πλοήγησης στο κάτω μέρος).

Επιστροφή στα σημεία ανάπτυξης

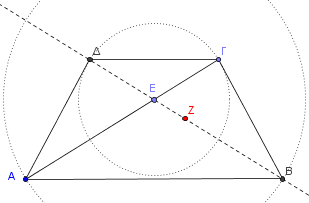
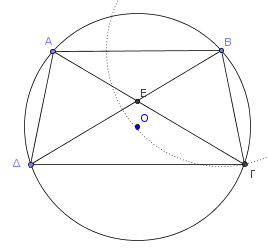
Η άσκηση που τους έθεσα για το σπίτι υποδείκνυε ακόμα έναν τρόπο για την κατασκευή ισοσκελούς τραπεζίου: Σε έναν κύκλο παίρνουμε ίσες χορδές ΑΔ και ΒΓ (παρακάτω σχήμα). Να αποδείξετε ότι το ΑΒΓΔ είναι είτε ορθογώνιο είτε ισοσκελές τραπέζιο.

Ουσιαστικά ζητάω να αποδείξουν την παραλληλία των ΑΒ και ΓΔ, κάτι που θα ήταν απλό, αν γνώριζαν την θεωρία για τις εγγεγραμμένες γωνίες. Χωρίς αυτήν τι μπορούν να κάνουν;

Μια ιδέα είναι η εξής: Έστω Ε το σημείο τομής των διαγωνίων ΑΓ και ΒΔ. Αν το Ε είναι το κέντρο του κύκλου, τότε εύκολα μπορούμε να δείξουμε ότι το ΑΒΓΔ είναι ορθογώνιο. Αν όχι, θα δείξουμε ότι είναι ισοσκελές τραπέζιο.

Ξεκινάμε με την ισότητα των διαγωνίων ΑΓ και ΒΔ. Αυτές είναι χορδές στα τόξα ΑΔΓ και ΒΓΔ, τα οποία όμως είναι ισα. Συνεπώς και οι χορδές τους θα είναι ίσες.

Τώρα είναι απλό να δούμε ότι ισχύουν οι ισότητες τριγώνων ΑΔΓ=ΒΔΓ και ΑΔΒ=ΑΓΒ, οι οποίες μας οδηγούν στην ισότητα των γωνιών ∠ΑΔΓ=∠ΒΔΓ και ∠ΑΔΒ=∠ΑΓΒ, συνεπώς και στην παραλληλία των ΑΒ και ΓΔ.

Δείτε την κατασκευή βήμα-βήμα (πατώντας τα βελάκια πλοήγησης στο κάτω μέρος).

Επιστροφή στα σημεία ανάπτυξης

Θα ήθελα να κλείσω με μερικές σκέψεις.

• Τα κατασκευαστικά προβλήματα βρίσκονται στον πυρήνα των γεωμετρικών θεμάτων και μπορούν να κινητοποιήσουν τους μαθητές.
• Είναι καλό να εκφράζονται εναλλακτικές ιδέες από τους μαθητές για ένα πρόβλημα, καθώς αυτό διευρύνει την αντίληψή τους και την οπτική τους για το θέμα. Χάρη σ' αυτή την πολυφωνία, οι μαθητές έλυσαν αρκετές ασκήσεις με ισοσκελή τραπέζια στο σχολείο.
• Το λογισμικό δυναμικής γεωμετρίας μπορεί να γίνει ένα νοητικό εργαλείο για τους μαθητές, όπως στην περίπτωσή μας ήταν ο έλεγχος μιας κατασκευής.Η γρήγορη κατασκευή (π.χ. η γρήγορη κατασκευή της μεσοκαθέτου) διευκολύνει αυτήν την διαδικασία ελέγχου και αναστοχασμού.
• Ο διαδραστικός πίνακας χρησιμοποιείται με ορθό τρόπο αν υποβοηθά την συλλογική διαπραγμάτευση.

Για να μην κουράσω τον αναγνώστη, δεν σημείωσα άλλες ενδιαφέρουσες παρεμβάσεις των μαθητών μου. Για παράδειγμα, παρατήρησαν πως όταν ενώσουμε τις μη-παράλληλες πλευρές ενός ισοσκελούς τραπεζίου, θα δημιουργηθεί ισοσκελές τρίγωνο.

Επιστροφή στα σημεία ανάπτυξης