ΕΝΟΤΗΤΕΣ

• Η έμπνευση για μια διαδραστική εφαρμογή GeoGebra
• Kατασκευή και ιδιότητες του σημείου Fermat
• Από τον καμβά της ζωγράφου στον καμβά του GeoGebra
• Σχετικοί σύνδεσμοι

Στα αγαπημένα βρήκα την ιστοσελίδα:
http://www.ams.org/mathimagery/displayimage.php?album=27&pid=322#top_display_media
Με κλικ πάνω της μαγεύτηκα από έναν πίνακα που περιείχε. Εντυπωσιάστηκα από την γεωμετρική μορφή του και τα χρώματα (τριχρωμία) και η εντύπωσή μου έγινε μεγαλύτερη όταν είδα τον τίτλο “ Fermat Point”. Αποφάσισα να δημιουργήσω τον πίνακα στο λογισμικό Geogebra, να αναδείξω τη γεωμετρία του, να κάνω την γεωμετρική κατασκευή και να περιγράψω τις σχετικές ιδιότητες.

Επισκεφθείτε τη διαδραστική εφαρμογή GeoGebra, κάνοντας κλικ επάνω στην εικόνα:

Για να μεταβείτε από τη μια διαφάνεια στην άλλη, πατήστε τους συνδέσμους (μαρκαρισμένες λέξεις με κίτρινο).

πρώτο       προηγούμενο       επόμενο       τελευταίο  Ορισμός Το Σημείο Φερμά-Τορικέλι είναι εσωτερικό σημείο ενός τριγώνου ΑΒΓ με γωνίες μικρότερες από 120o από το οποίο το άθροισμα των αποστάσεων από τις κορυφές του τριγώνου είναι ελάχιστο. Για να κατασκευάσουμε το σημείο Fermat Με πλευρές ΑΒ, ΑΓ και ΒΓ κατασκευάζουμε ισόπλευρα τρίγωνα εξωτερικά του τριγώνου ΑΒΓ. Για να κατασκευάσουμε το σημείο Fermat Σχεδιάζουμε τα ευθ. τμήματα ΑΑ', ΒΒ' και ΓΓ'. Για να κατασκευάσουμε το σημείο Fermat Το σημείο τομής των ευθ. τμημάτων ΑΑ', ΒΒ' και ΓΓ' είναι το σημείο Fermat. Για να κατασκευάσουμε το σημείο Fermat Ένας άλλος τρόπος είναι να κατασκευάσουμε τους περιγεγραμμένους κύκλους των ισοπλεύρων τριγώνων. Το σημείο που τέμνονται είναι το σημείο Fermat. Ιδιότητες Η βασική ιδιότητα είναι ότι το άθροισμα FA+FB+FΓ είναι ελάχιστο. Επί πλέον: 1) ΑΑ'= ΒΒ'=ΓΓ' 2) Ειδικότερα FA+FB+FΓ=ΑΑ'=ΒΒ'=ΓΓ' 3) Για τις γωνίες ∠AFB=∠BFΓ=∠ΓFA=120o Σκιαγράφηση της απόδειξης των ιδιοτήτων 1-3 Ας υποθέσουμε ότι σχεδιάσαμε το ισόπλευρο τρίγωνο πλευράς ΒΓ, τον περιγεγραμμένο κύκλο του τριγώνου και το F ας είναι τυχαίο σημείο στο τόξο ΒΓ. Τότε οι εγγεγραμμένες γωνίες ∠Α'FΓ και ∠A'FB είναι 60o αφού βαίνουν σε τόξα 120o. Κατά συνέπεια, ∠ΒFΓ=120o (αυτό έπεται και από το γεγονός ότι η γωνία ∠ΒFΓ είναι η απέναντι της ∠ΒΑ'Γ στο εγγεγραμμένο τετράπλευρο Α'ΒFΓ). Σκιαγράφηση της απόδειξης των ιδιοτήτων 1-3 Αν τώρα προεκτείνουμε την FΓ κατά τμήμα ΓΡ ίσο με ΒF παρατηρούμε ότι τα τρίγωνα Α'ΒF και Α'ΓΡ είναι ίσα (αφού στο εγγεγραμμένο τετράπλευρο Α'ΒFΓ η γωνία ∠Β ισούται με την ∠Γεξ). Συνεπώς, το τρίγωνο Α'FP είναι ισόπλευρο (ισοσκελές με την γωνία ∠F=60o). Αυτό αποδεικνύει ότι FB+FΓ=FA' Σκιαγράφηση της απόδειξης των ιδιοτήτων 1-3 Ας επιστρέψουμε στο τρίγωνο και ας σχεδιάσουμε μόνο δύο ισόπλευρα τρίγωνα (π.χ. με πλευρές τις ΒΓ και ΒΑ). Οι περιγεγραμμένοι κύκλοι θα τέμνονται εκτός από το Β και σε δεύτερο σημείο, έστω F. Τότε οι γωνίες ∠ΒFΓ=∠ΒFA=120o. Κατά συνέπεια, και η γωνία ∠BFΑ=120o. (Αναγκαστικά δηλαδή και ο τρίτος κύκλος θα διέλθει από το F). Επίσης, εφόσον η γωνία ∠BFA'=60o, τα σημεία A, F, A' είναι συνευθεικά και μάλιστα AA'=FΓ+FB+FA.

Όπως ο ζωγράφος χρησιμοποιεί τον καμβά για βάση του πίνακά του έτσι ο καμβάς στην προκειμένη περίπτωση είναι το παράθυρο γραφικά του λογισμικού. Για να μπορέσω να «παίξω» με τα χρώματα του φόντου δημιούργησα ένα τετράπλευρο με κορυφές τις κορυφές του παραθύρου των γραφικών.
Υπάρχει η εντολή ΚορυφήΓραφικών[<Αριθμός της κορυφής>]

• 1^ο στάδιο κατασκευής:

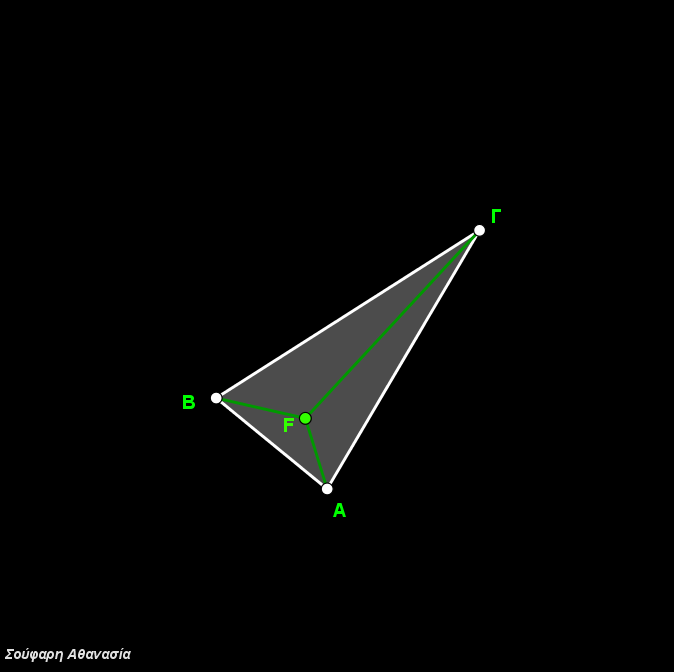
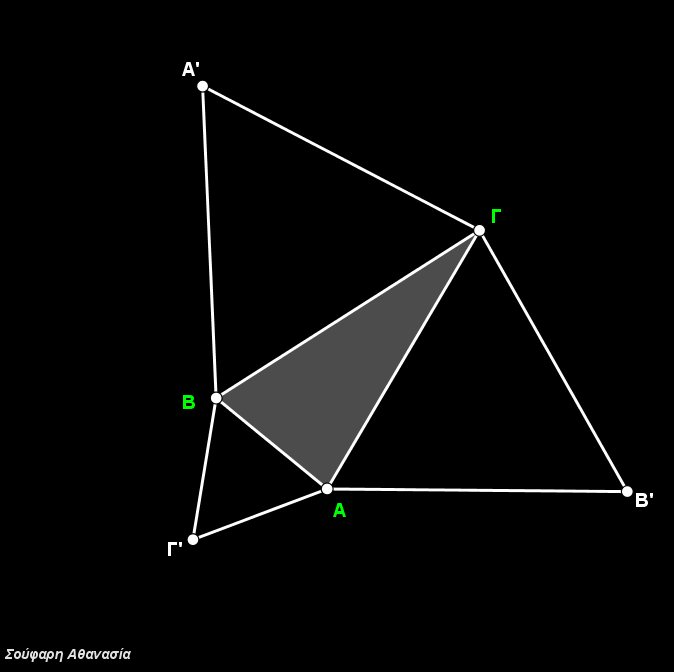
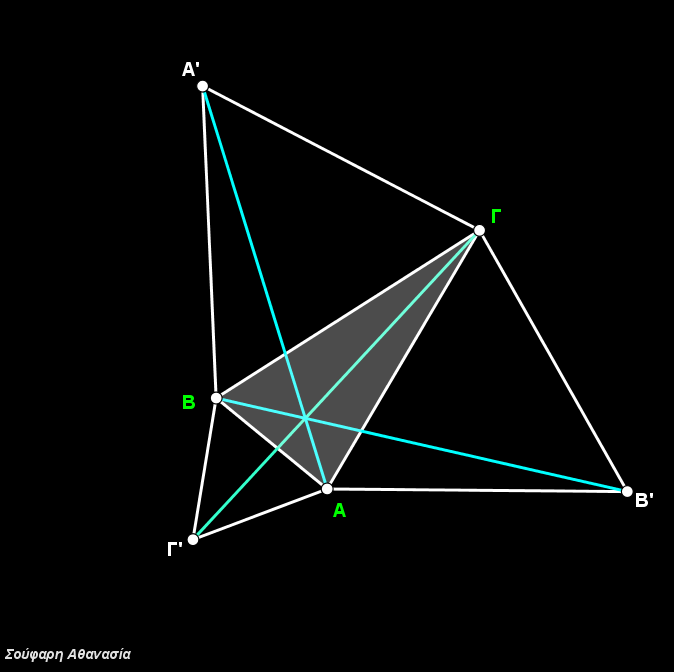
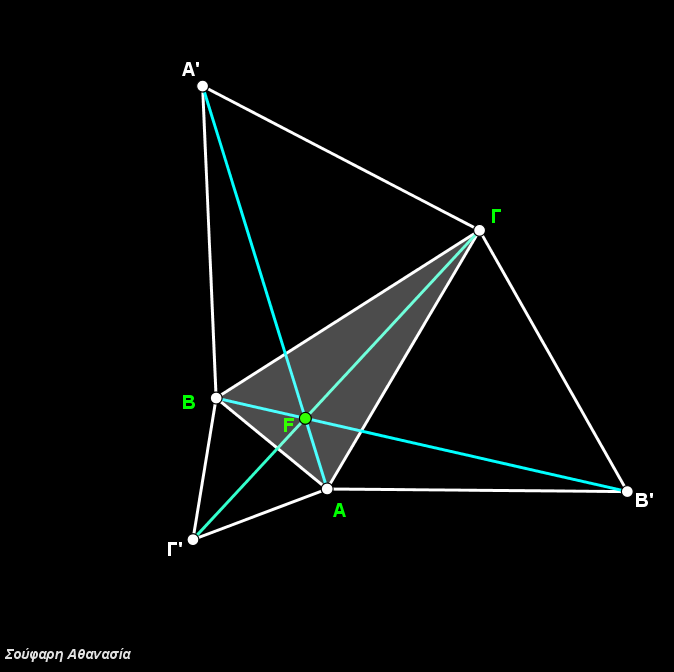
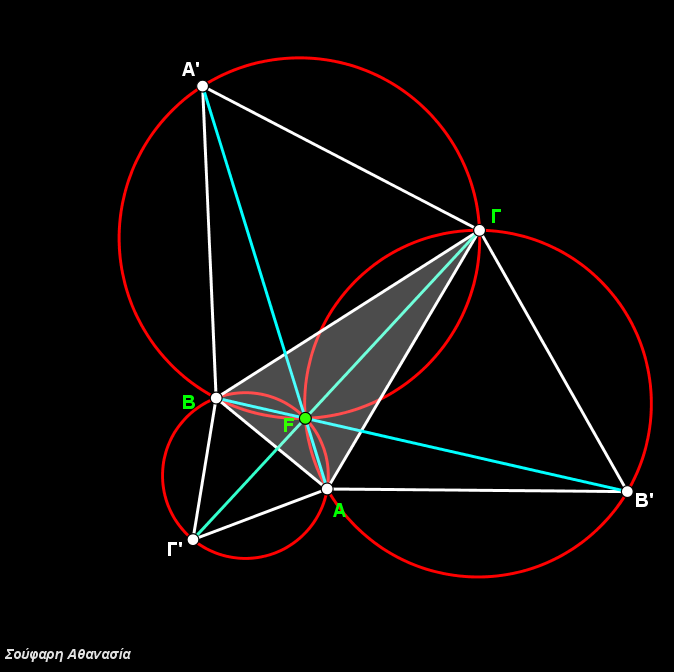
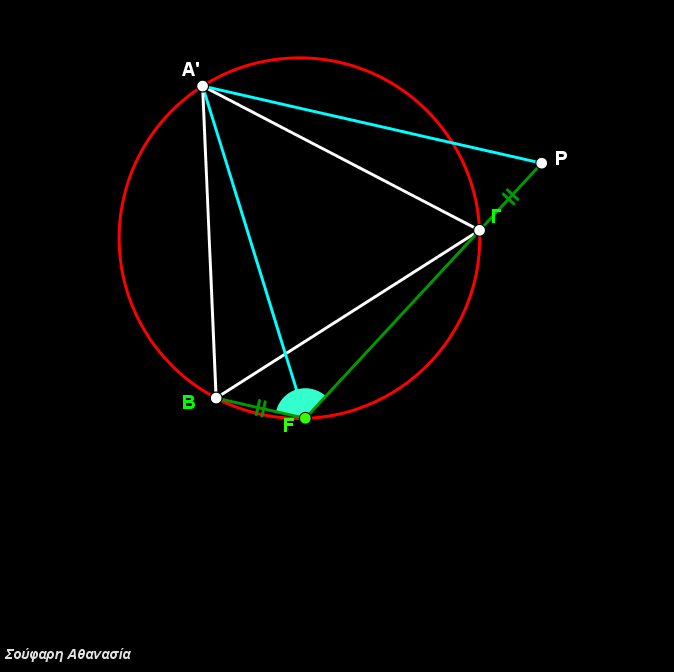
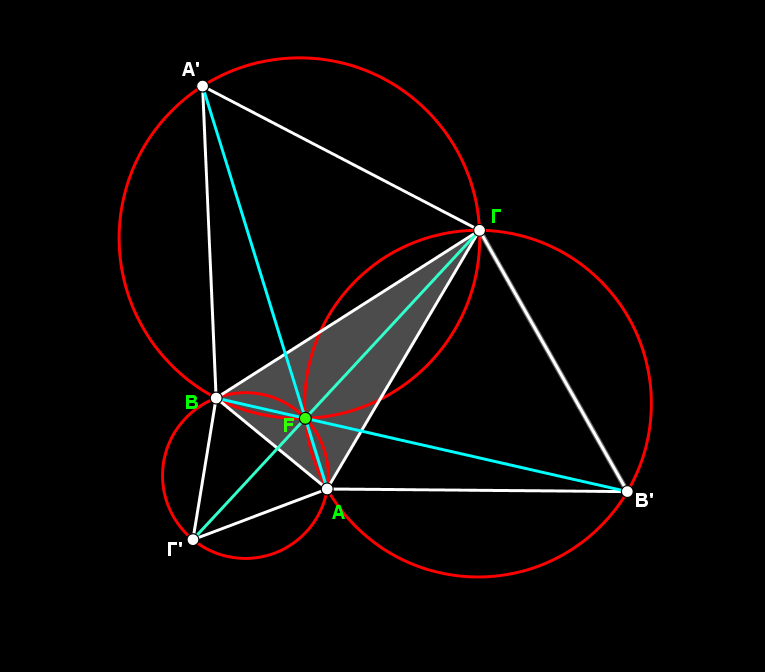
  Κατασκευάστηκε το τρίγωνο ΑΒΓ , τα ισόπλευρα τρίγωνα ΒΓΑ’, ΓΑΒ’, ΑΒΓ’ καθώς και οι περιγεγραμμένοι κύκλοι τους και τα ευθ. τμήματα ΑΑ’, ΒΒ’ και ΓΓ’.

  Η τομή των περιγεγραμμένων κύκλων που ταυτίζεται με την τομή των ευθ. τμημάτων ΑΑ’, ΒΒ’ και ΓΓ’ ορίζει το σημείο Fermat F.

  
• 2^ο στάδιο κατασκευής:

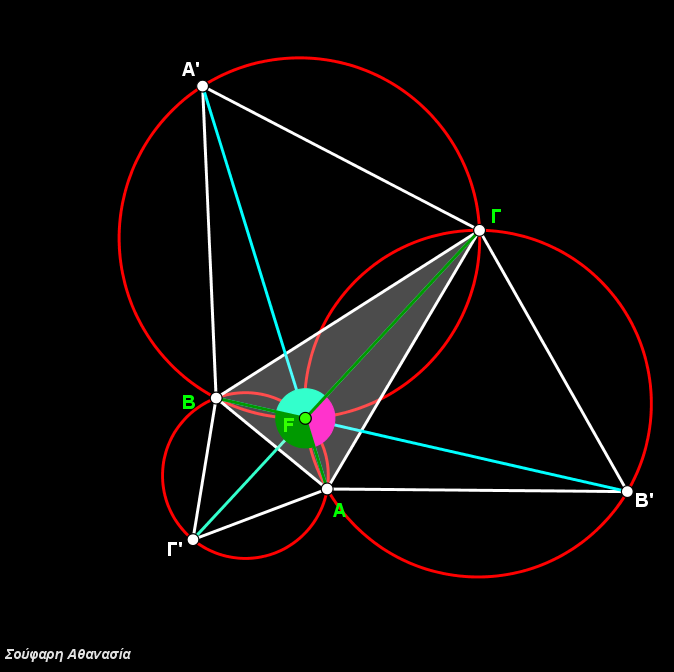
  Το σχήμα είναι μια σύνθεση γεωμετρικών σχημάτων και ειδικά πολυγώνων και κυκλικών τμημάτων. Προσπάθησα να αναπαράγω τον πίνακα με τα χρώματα που είχε (τριχρωμία) και ακολουθώντας τον κανόνα που η ζωγράφος είχε επιλέξει να χρωματίσει τα γεωμετρικά σχέδια.

  Τα κυκλικά τμήματα δημιουργήθηκαν με «γέμισμα» ( αδιαφάνεια 100%) των αντίστοιχων τόξων τους.

  Κάθε κύκλος έχει τριχρωμία. Τρίγωνα που “επικοινωνούν” με κατακορυφήν γωνίες έχουν ίδιο χρώμα.

  Το πρόβλημα της επικάλυψης του ενός χρώματος από το άλλο λύθηκε με τη χρήση επιπέδων στρώσης. Π.χ. το κυκλικό τμήμα που καλύπτει μια περιοχή ενός τριγώνου πρέπει να κατασκευαστεί με επίπεδο στρώσης μεγαλύτερης αυτής του τριγώνου.

  Επισυνάπτω αρχείο Geogebra (Fermat_by_steps.ggb) που εξηγεί το «παιχνίδι» με τα χρώματα.

  

• Σημείο Fermat και Τέχνη, της Αθανασίας Σούφαρη (GeoGebra Tube)
• Suman Vaze: Mathematical Artwork
• "Fermat Point," by Suman Vaze (King George V School, Hong Kong), Mathematical Imagery (AMS - American Mathematical Society)
• Σημείο Fermat (Όλη η μελέτη), του Δημήτρη Μυρογιάννη
• Σημείο Fermat, του Κώστα Παπαστεργίου (YouTube)
• Πως με την γεωμετρία γλυτώνεις χρήματα…, του Αθανασίου Δρούγα (ΜΑΘΗ Μαγικά)