UNITS

• The inspiration for an interactive GeoGebra application
• Construction and properties of the Fermat Point
• From the painter's canvas to the GeoGebra canvas
• Relative Links

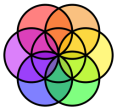
On the catalogue of my favourite pages I found the web-page:
http://www.ams.org/mathimagery/displayimage.php?album=27&pid=322#top_display_media
When I visited the site, I was caught by a painting published there. It impressed me with its geometric structure and its three color palette. But I was impressed even more by its title “Fermat Point”. I decided to construct the painting on the GeoGebra canvas using geometric construction tools, aiming to highlight its geometry and to describe its geometric properties.

Click on the picture below to open the interactive GeoGebra application.

Back to top

To navigate from one slide to the other, just click on the links (highlighted words).

first       previous       next       last  Definition The Fermat-Torricelli Point is an inner point of a triangle ΑΒΓ with angles less than 120o with the property that the sum of its distances from the triangle vertices is minimal. How to construct the Fermat Point We construct equilateral triangles with sides ΑΒ, ΑΓ and ΒΓ outside of the triangle ΑΒΓ. How to construct the Fermat Point We then draw the segments ΑΑ', ΒΒ' and ΓΓ'. How to construct the Fermat Point The point where ΑΑ', ΒΒ' and ΓΓ' intersect is the Fermat Point. How to construct the Fermat Point Alternatively, we can construct the circumscribed circles of the equilateral triangles. Their intersection point is the Fermat Point. Properties The main property of the Fermat Point is that the sum FA+FB+FΓ becomes minimal. More over: 1) ΑΑ'= ΒΒ'=ΓΓ' 2) More precisely FA+FB+FΓ=ΑΑ'=ΒΒ'=ΓΓ' 3) And for the angles it holds that ∠AFB=∠BFΓ=∠ΓFA=120o A draft of the proof of the 1-3 properties Supose we just draw the equilateral triangle with side ΒΓ, its circumscribed circle and let F be any point on the arc ΒΓ. Then, the inscribed angles ∠Α'FΓ and ∠A'FB are equal to 60o since their corresponding arcs are 120o. This implies that, ∠ΒFΓ=120o (it also follows from the fact that the angle ∠ΒFΓ is oposite of the angle ∠ΒΑ'Γ on the inscribed quadrilateral Α'ΒFΓ). A draft of the proof of the 1-3 properties If we extend FΓ to a segment ΓΡ equal to ΒF we notice that triangles Α'ΒF and Α'ΓΡ are equal (since that on the inscribed quadrilateral Α'ΒFΓ the angle ∠Β equals to the angle ∠Γexterior). Thus, the triangle Α'FP is equilateral (isosceles with the angle ∠F=60o). And that proves the equation FB+FΓ=FA' A draft of the proof of the 1-3 properties Let's go back to the triangle and draw just the two equilateral triangles (say with sides ΒΓ and ΒΑ). The circumscribed circles will intersect apart from Β also to another point, say F. Then the angles ∠ΒFΓ=∠ΒFA=120o. It then follows that also ∠BFΑ=120o. (That forces the third circle to pass through F as well). Also, since the angle ∠BFA'=60o, points A, F and A' are collinear and they justify the equation AA'=FΓ+FB+FA.

Back to top

Just like a painter’s canvas is the base of a painting, the “graphics window” on the GeoGebra software is the base of a geometric construction. In order to “play” with the colors, I created a quite big quadrilateral on the background, covering the graphics window.
There is the command Corner[ ]

• 1^st stage of the construction:

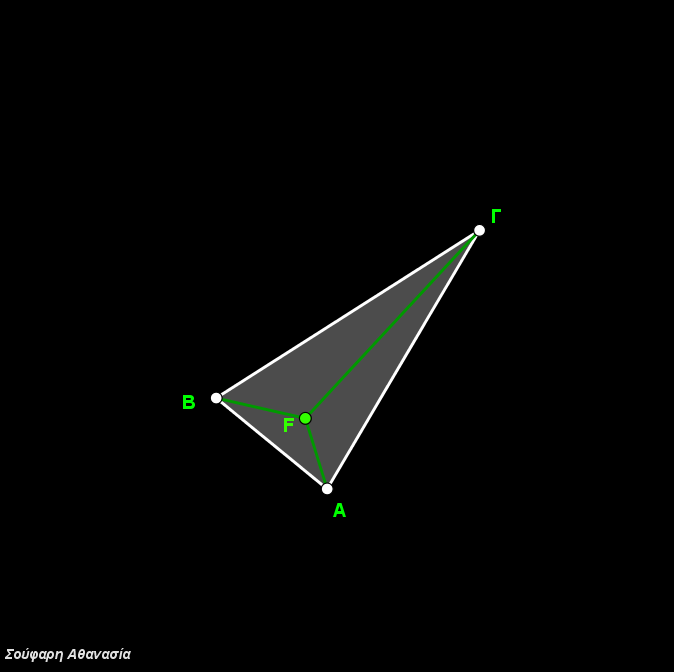
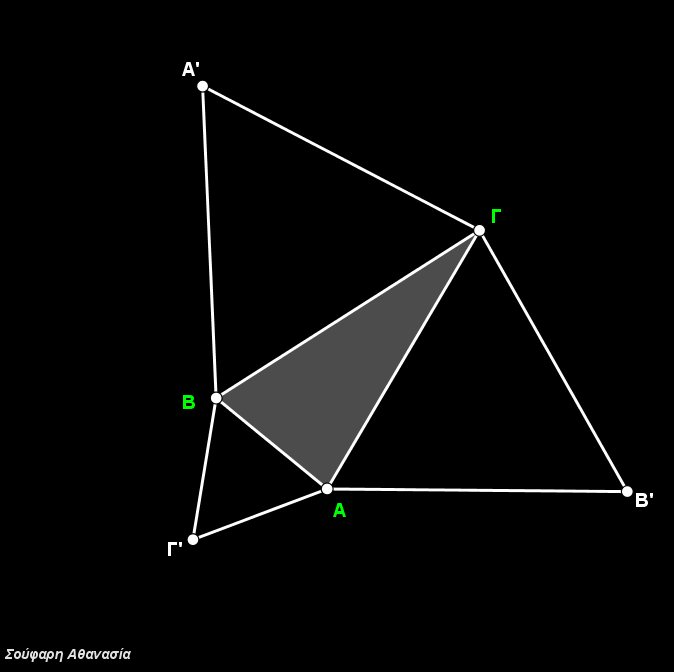
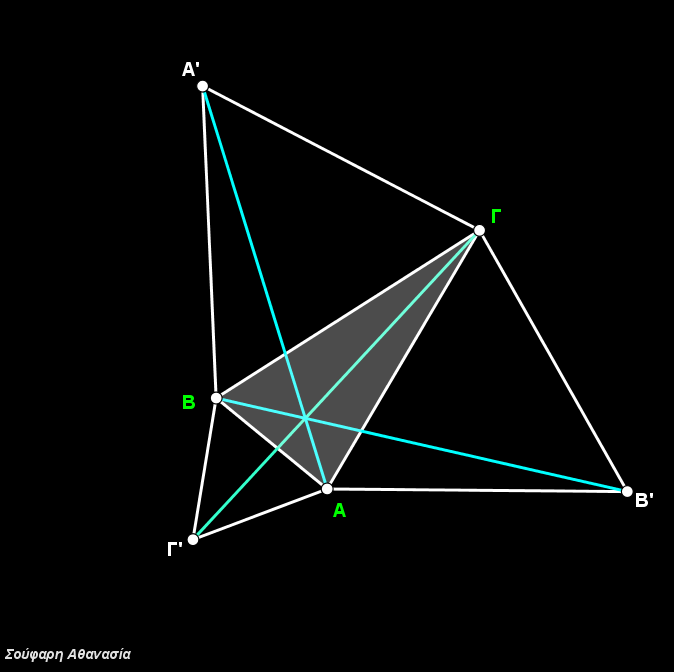
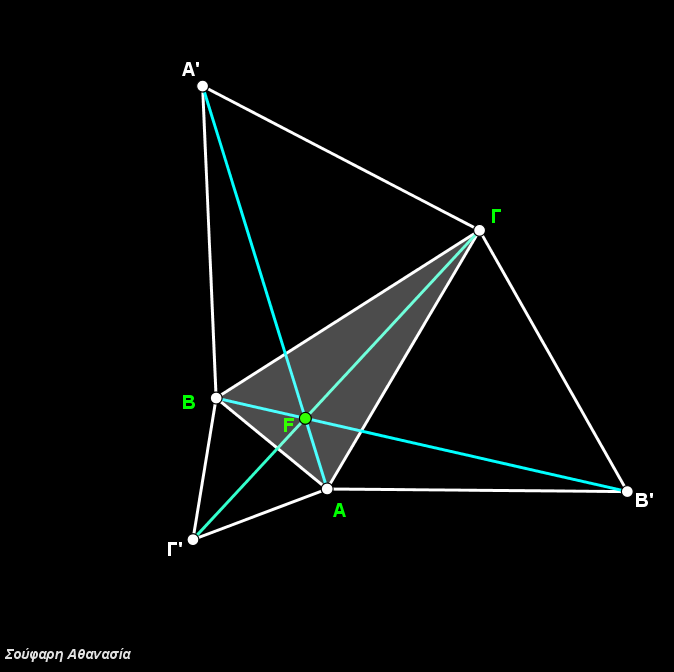
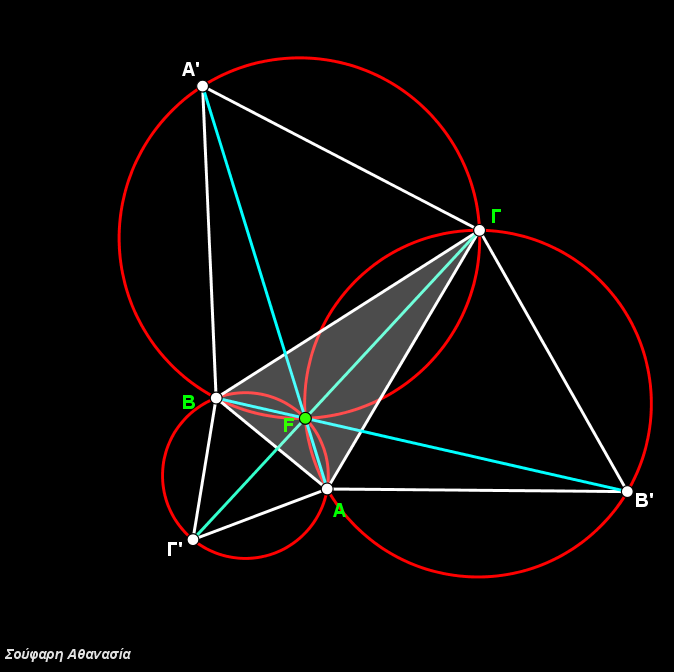
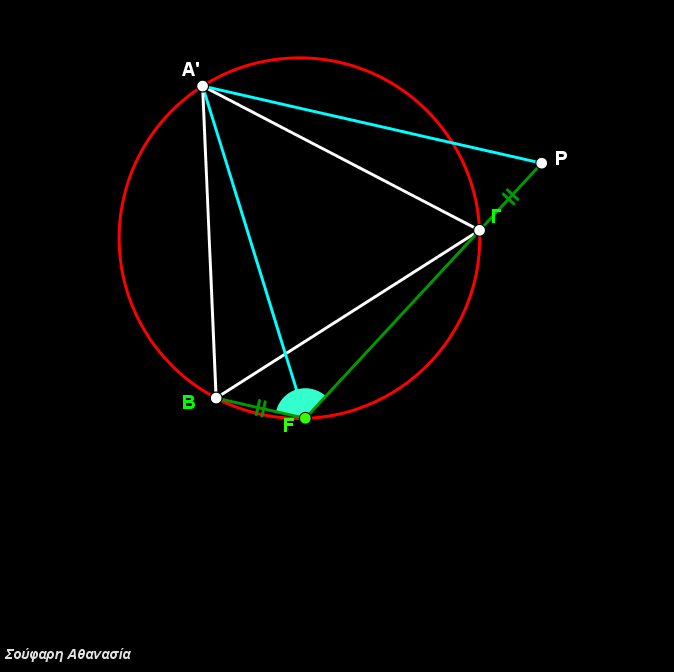
  I constructed the triangle ΑΒΓ, the equilateral triangles ΒΓΑ’, ΓΑΒ’, ΑΒΓ’, their circumscribed circles and the line segments ΑΑ’, ΒΒ’ and ΓΓ’.

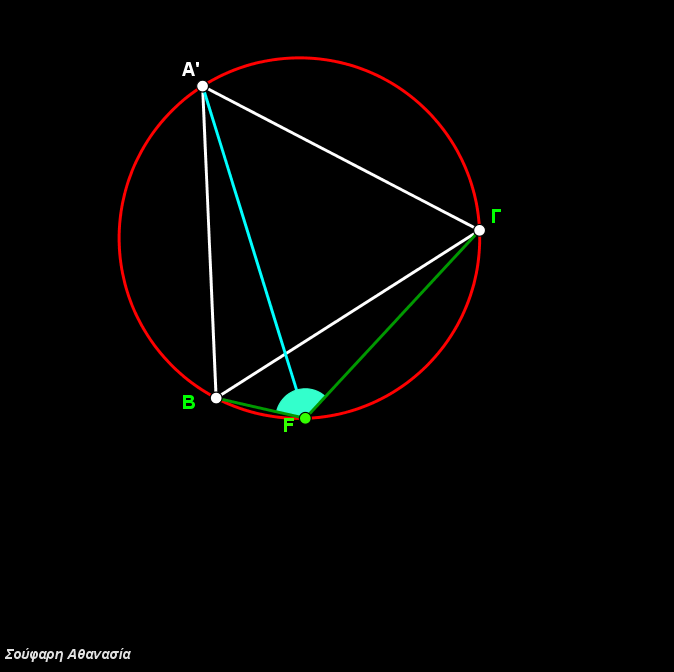
  The intersection of the three circumscribed circles, which is identical to the intersection of the three line segments ΑΑ’, ΒΒ’ and ΓΓ define the Fermat Point F.

  
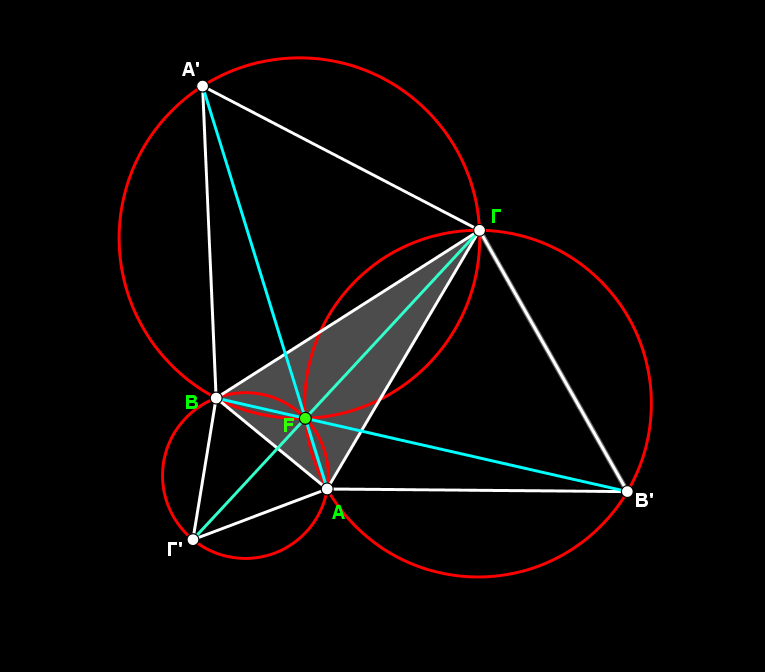
• 2^nd stage of the construction:

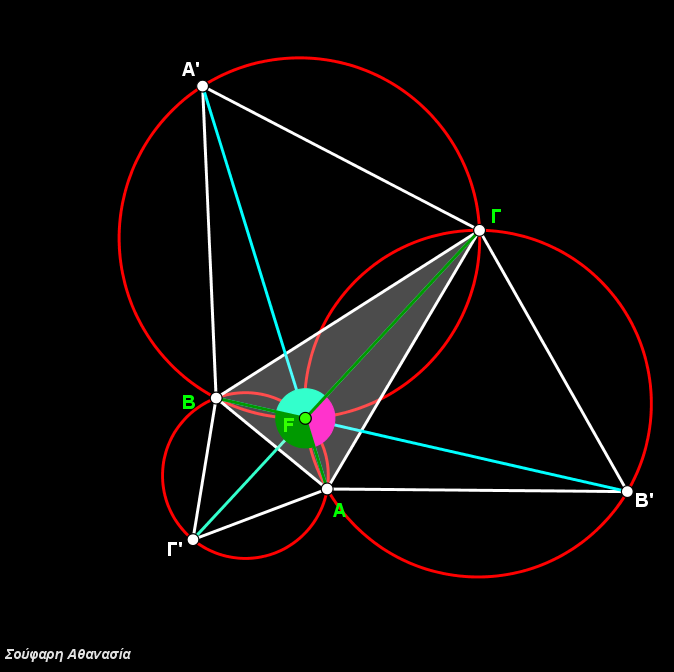
  The painting is a synthesis of geometric shapes (polygons and circular segments). I tried to reproduce the painting with its palette (three colors) and the coloring rules set by the painter Suman Vaze.

  The circular segments where created by filling arcs (opacity 100%).

  In each circle we meet all three colors. When triangles form vertical angles they have the same color.

  The problem of the overlapping colors was solved by using layers. For instance, a circular segment that covers a part of a triangle should be placed on an upper layer, above of the triangle.

  Find attached a GeoGebra file (Fermat_by_steps.ggb) that explains the “coloring game”.

  

Back to top

• Fermat Point and Art, by Athanasia Soufari (GeoGebra Tube)
• Suman Vaze: Mathematical Artwork
• "Fermat Point," by Suman Vaze (King George V School, Hong Kong), Mathematical Imagery (AMS - American Mathematical Society)
• Fermat Point (The whole study), by Dimitris Myrogiannis
• Fermat Point, by Kostas Papastergiou (YouTube)
• How the geometry saves you money…, by Athanasios Drougas (MATH Magic)

Back to top