Λέμε πως μια ποσότητα φθίνει εκθετικά όταν μειώνεται με ρυθμό ανάλογο με την τρέχουσα τιμή της. Εναλλακτικά, μπορούμε να σκεφτούμε την εκθετική απόσβεση ως εξής: ο χρόνος που απαιτείται για τον υποδιπλασιαμό μιας ποσότητας είναι πάντα ο ίδιος και ανεξάρτητος από την αρχική ποσότητα. Αυτός ο χρόνος ονομάζεται "χρόνος ημίσειας ζωής" ή απλώς "ημιζωή". Τα πιο συνηθισμένα παραδείγματα ποσοτήτων που αποσβαίνουν εκθετικά είναι τα ραδιενεργά ισότοπα. Για παράδειγμα ο Φώσφορος-32 έχει χρόνο ημιζωής 14 ημέρες. Αυτό σημαίνει ότι αν έχουμε μια αρχική ποσότητα Φωσφόρου-32, έστω Q₀, τότε, μετά από 14 μέρες η ποσότητα που θα έχει απομείνει θα είναι ½Q₀. Στο σχολικό βιβλίο υπάρχει μια μικρή λίστα με ραδιενεργά ισότοπα και τον χρόνο ημιζωής τους. Την παραθέτουμε παρακάτω.

Πραγματικά, ενθουσιαζόμαστε ιδιαίτερα όταν η σχολική άλγεβρα συναντά κάποιες εφαρμογές στον πραγματικό κόσμο, όπως στην περίπτωση της εκθετικής απόσβεσης. Είναι όμως μονάχα μια εγκυκλοπαιδική γνώση; Πώς θα μπορούσαμε να ενεργοποιήσουμε τους μαθητές μας ώστε να πειραματιστούν με ποσότητες που αποσβαίνουν εκθετικά και να εντοπίσουν τον σωστό νόμο εκθετικής μεταβολής; Πήρα την απάντησή μου από μια συνάδελφο, την Πότα Κοταρίνου, που έγραψε ένα υπέροχο σενάριο με τίτλο "Τα σοκολατάκια και ο νόμος της εκθετικής μεταβολής". Αυτό το σενάριο εφαρμόσαμε στην τάξη, με δύο τμήματα: το Β2 και το Β3 στις 4 Απριβλίου 2016.

Το πείραμα οργανώθηκε σε 7 στάδια:

• 1^ο στάδιο: Κάθε τμήμα χωρίστηκε σε 3 ομάδες των 6 μαθητών περίπου. Οι ομάδες έλαβαν από ένα χάρτινο κύπελλο σφραγισμένο με καπάκι -που περιείχε ακριβώς 100 σοκολατάκια m&ms- και ένα πλαστικό πιάτο.
• 2^ο στάδιο: Κάθε ομάδα, αφού ταρακουνούσε καλά το κύπελλο, άπλωνε το περιεχόμενό του στο πιάτο. Έπειτα, προσέχοντας να μην αναποδογυρίσουν τα σοκολατάκια, επέλεγαν εκείνα που δεν έφεραν επιγραφή στο πάνω μέρος (καθώς την έφεραν στο κάτω μέρος) και τα "εξάλειφαν". Φαντάζεστε πόσο νόστιμη ήταν η διαδικασία της εξάλειψης!
  
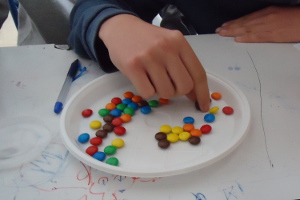
• 3^ο στάδιο: Μόλις η εξάλειψη ολοκληρωνόταν, οι μαθητές μετρούσαν όσα σοκολατάκια είχαν απομείνει, τα οποία επανατοποθετούσαν μέσα στο κύπελλο.
• 4^ο στάδιο: Επαναλάμβαναν τα στάδια 2 και 3 όσες φορές χρειαζόταν μέχρι να εξαλειφθεί και το τελευταίο σοκολατάκι.
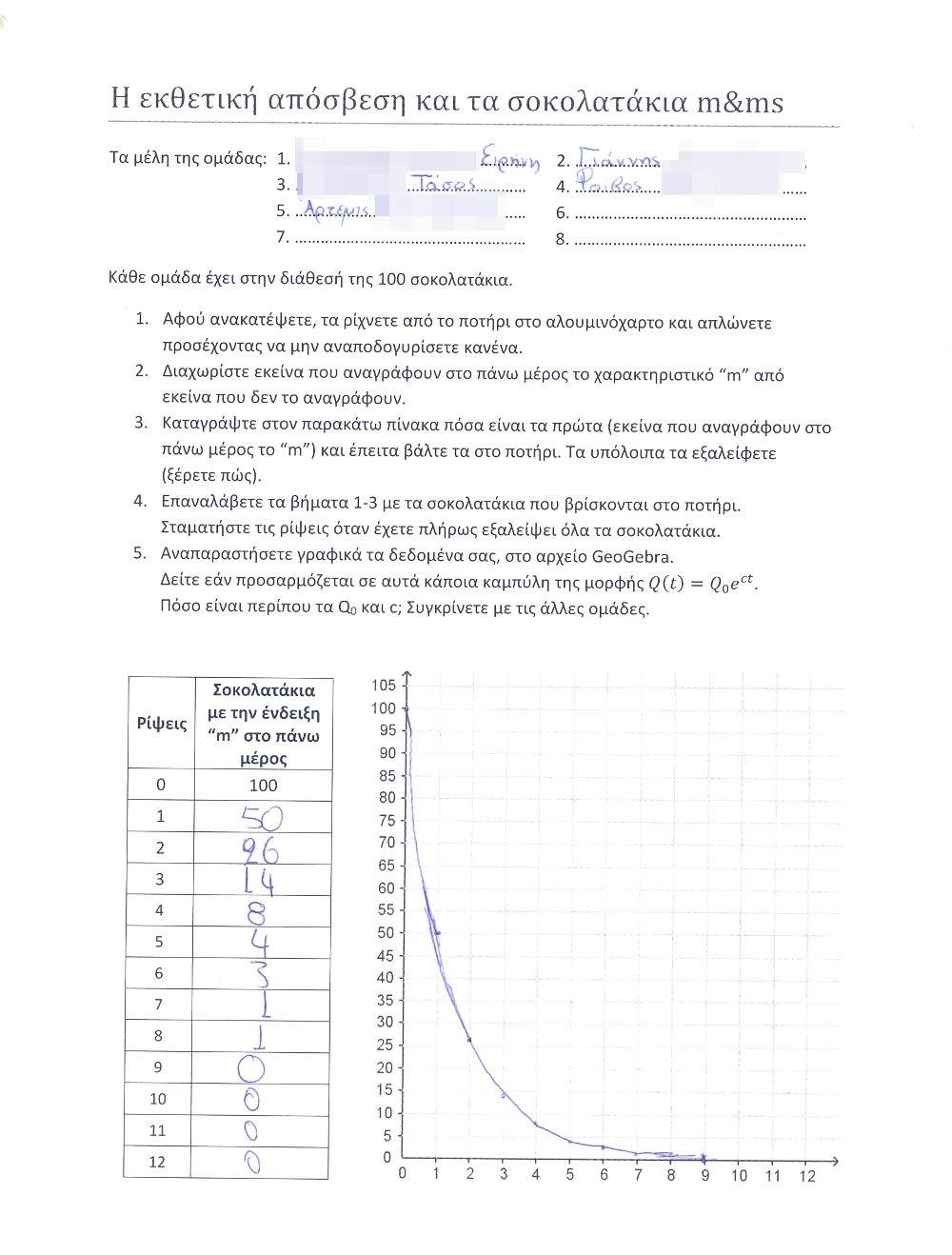
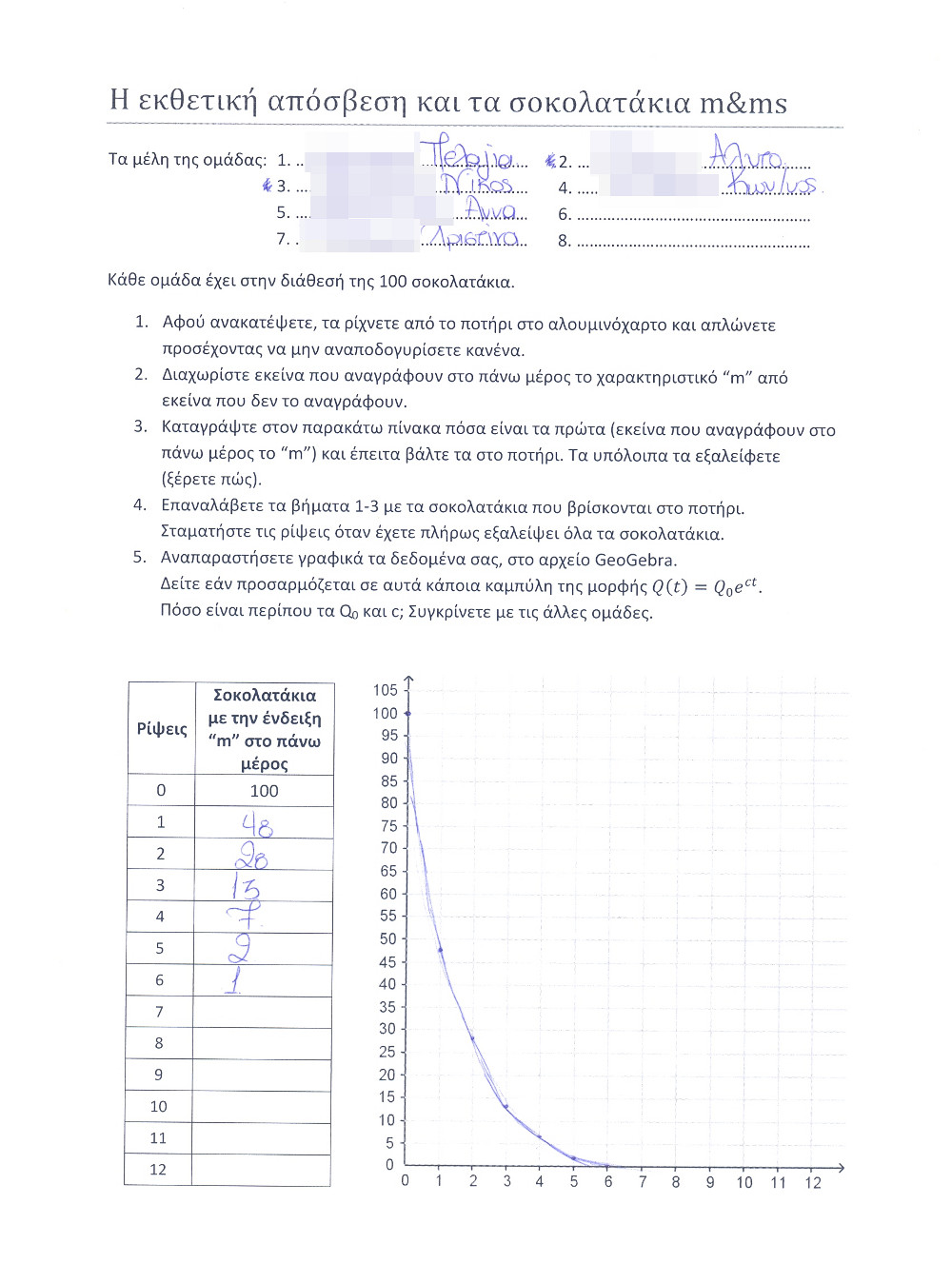
• 5^ο στάδιο: Κάθε ομάδα κλήθηκε να συμπληρώσει έναν πίνακα με δύο στήλες: η πρώτη αριθμούσε τις ρίψεις των σοκολάτων, ξεκινώντας από το 0, και η δεύτερη ήταν για τον ακριβή αριθμό σοκολάτων που απέμειναν μετά την διαδικασία εξάλειψης.
• 6^ο στάδιο: Τα ζεύγη των αριθμών (#ρίψη, πλήθος σοκολάτων) σημειώνονταν σε ένα γράφημα (χρησιμοποιήσαμε το λογιστικό φύλλο του GeoGebra) και οι μαθητές προσπαθούσαν να προσαρμόσουν σε αυτά μια εκθετική απόσβεση. Ήταν πραγματικά εκπληκτικό το γεγονός ότι σχεδόν σε όλα τα πειράματα η καλύτερη προσαρμογή γινόταν με την συνάρτηση Q(t)=100e^-0.7t!
  
• 7^ο στάδιο: Τέλος, κάθε ομάδα παρουσίασε την εργασία της στις υπόλοιπες.

Βρείτε παρακάτω μερικά σλάιντ με σχόλια και τα συμπληρωμένα φύλλα εργασίας κάθε ομάδας.

Η πρώτη μας ρίψη! 100 m&ms!

Τα απλώνουμε καλά στο πιάτο.

Ας μαζέψουμε εκείνα τα m&ms
που δεν έχουν επιγραφές στο πάνω μέρος.

Τα εξαλείφουμε
και τα υπόλοιπα επιστρέφουν στο κύπελλο.

Συνεχίζουμε να ρίπτουμε και να εξαλείφουμε
μέχρι να τα αφανίσουμε όλα!

Ώρα να συμπληρώσουμε το φυλλάδιο,

και να εντοπίσουμε τον σωστό νόμο εκθετικής απόσβεσης.

Η σειρά μας τώρα, το B3,
μελετάμε το πειραματικό υλικό μας.

Mμμμ μπόλικα m&ms!

Όλοι θέλουμε να εξαλείψουμε μερικά σοκολατάκια!

Δεύτερος γύρος.

Τελειώνουμε όπου νά 'ναι.

Πάει και το φύλλο εργασίας.

Και τώρα στον υπολογιστή να εντοπίσουμε
την πιο καλά προσαρμοσμένη εκθετική απόσβεση.

1 2 3 4 5 6 7 8 9 10 11 12 13 14

Συμπληρωμένα ομαδικά φύλλα εργασίας

• B2, πρώτη ομάδα
  
• B2, δεύτερη ομάδα
  
• B2, τρίτη ομάδα
  
• B3, πρώτη ομάδα
  
• B3, δεύτερη ομάδα
  
• B3, τρίτη ομάδα
  

Επιπλέον υλικό του μαθήματος

• Εισαγωγική παρουσίαση για την εκθετική μεταβολή (pps)
• Τρία αρχεία GeoGebra: Η εκθετική μεταβολή (ggb), Τα σοκολατάκια m&ms (ggb), Ο ναυτίλος (ggb)
• Κενό φύλλο εργασίας ομάδων (pdf)

• Αποθετήριο Ιφιγένεια: Τα σοκολατάκια και ο νόμος της εκθετικής μεταβολής της Πότας Κοταρίνου (δημοσιευμένο από τον Γιώργο Ψυχάρη)