Η ιστορία μας ξεκινά τον χειμώνα,
λίγο πριν τα Χριστούγεννα,

φτιάχνοντας τα πρώτα τετράεδρα,
με χαρτοδιπλωτική.

Όταν συγκεντρώσαμε πολλά τετράεδρα
κατά τον Μάη,

πέσαμε με τα μούτρα στη δουλειά!

Τέσσερα μικρά τετράεδρα
χτίζουν ένα μεγαλύτερο!

Νάτο!
Δεν είναι ωραίο;

...και τέσσερα από αυτά τα λίγο μεγαλύτερα

χτίζουν ένα ακόμα πιο μεγάλο

Τέλειο;

Ας το καμαρώσουμε!

Σιγά-σιγά άρχισαν να μαζεύονται μερικά

Τώρα έχουμε οχτώ.
Είναι αρκετά για να...

...χτίσουν δύο ΠΟΛΥ ΜΕΓΑΛΑ τετράεδρα!

Θυμάστε τα δύο ΠΟΛΥ ΜΕΓΑΛΑ τετράεδρα;
Πάμε για άλλα δύο!

Εμπρός λοιπόν!
Ξεκινάμε με μικρά τετράεδρα.

Δείτε πόσοι δουλεύουμε!
Εδώ δεν κάνουμε αστεία!

Κι ο κ. Συγκελάκης φυσικά!

Μάθημα Γεωμετρίας
αλλά και δεξιοτεχνίας!

Τα "ακόμα πιο μεγάλα" τετράεδρα ξεκίνησαν!

Εδώ άλλο ένα!
Πήραμε φόρα! Φτιάξαμε εννέα τέτοια!

Οι φιναλίστ της ημέρας.
Χτίζουν τα ΠΟΛΥ ΜΕΓΑΛΑ τετράεδρα.

Διακρίνετε τα διαφορετικά τετράεδρα
ή χαθήκατε στην πολυχρωμία;

Τελευταίες πινελιές!
(μάλλον σελοτέιπ)

Και τώρα η μεγάλη στιγμή!

Με τέσσερα ΠΟΛΥ ΜΕΓΑΛΑ τετράεδρα
χτίσαμε το τετράεδρο του Sierpinski!

Αναμνηστική φωτο 1:
To A₂ με το τετράεδρο Sierpinski.

Αναμνηστική φωτο 2:
To A₃ με το τετράεδρο Sierpinski.

Το τετράεδρο του Sierpinski.
Μήπως να φτιάξουμε άλλα τρία;

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28

Πλησίαζαν Χριστούγεννα του 2013 και υπήρχε θετικό κλίμα για κατασκευές και διακοσμήσεις. Τότε συλλάβαμε την ιδέα να φτιάξουμε ένα δέντρο -ένα «μαθηματικό» δέντρο- που μονάχα η θέα του να προκαλεί τη λογική. Αλλά δεν θέλαμε οι μαθητές μας να είναι απλώς θεατές. Επιθυμούσαμε να έχουν τον πρωταγωνιστικό ρόλο του δημιουργού.

Η αναζήτηση μιας τέτοιας δραστηριότητας, μάς οδήγησε στο τετράεδρο του Sierpinski. Η ιδέα ήταν απλή: οι μαθητές θα κατασκεύαζαν με χαρτί πολλά, μικρά, ίσα τετράεδρα και έπειτα θα τα συνένωναν με σελοτέιπ για να δομήσουν το τετράεδρο του Sierpinski. Με αυτόν τον τρόπο, θα εμπλέκονταν σε διαδικασία άτυπης μάθησης μαθηματικών εννοιών όπως «ισόπλευρο τρίγωνο», «τετράεδρο», «fractal», «επαγωγή» (η κατασκευή γίνεται επαγωγικά), «γεωμετρική πρόοδος», «εκθετική αύξηση». Το εύρος μεγάλο και όχι περιορισμένο στο Αναλυτικό Πρόγραμμα κάποιας Τάξης. Συνεπώς το γνωστικό όφελος θα ήταν μεγαλύτερο για εκείνους που αγνοούσαν πλήρως αυτές τις έννοιες, και αυτοί ήταν οι μαθητές της Α’ Λυκείου, τα τμήματα Α₂ και Α₃.

Σύντομα λήφθησαν διάφορες αποφάσεις, όπως το να κατασκευαστούν τα τετράεδρα-δομικοί λίθοι με χαρτοδιπλωτική, να αφήσουμε τους μαθητές να επιλέξουν χρωματισμούς και συνδυασμούς, να εντάξουμε τη δραστηριότητα στις ώρες των μαθημάτων μας.

Ακολούθησε η εφαρμογή σε δυο φάσεις: Αρχικά, αφιερώσαμε μια διδακτική ώρα σε κάθε τμήμα για να διδάξουμε την κατασκευή του τετραέδρου-δομικού λίθου με χαρτοδιπλωτική. Εκείνη την ώρα κατασκευάστηκαν μερικά τετράεδρα, όχι όμως αρκετά για να προχωρήσουμε στο επόμενο στάδιο της κατασκευής. Αναγκαστικά έπρεπε να περιμένουμε τους μαθητές να ετοιμάσουν περισσότερα τετράεδρα στο σπίτι τους.

Όμως η αναμονή ήταν πολύ μεγαλύτερη, καθώς δόθηκε προτεραιότητα στη διδασκαλία της εξεταστέας ύλης. Εν τέλει, κατά τα μέσα Μαΐου, μπορέσαμε να «ξεκλέψουμε» ένα δίωρο από τα μαθήματά μας για τη δεύτερη φάση, της επαγωγικής δόμησης του τετραέδρου του Sierpinski.

Ήταν κάτι που οι μαθητές σχεδόν το περίμεναν. Κατά τη διάρκεια της κατασκευής, κάθε φορά που εμφανιζόταν ένα τετράεδρο μεγαλύτερης κλάσης από αυτά που είχαν ήδη κατασκευαστεί, ακούγονταν φωνές ενθουσιασμού. Η συγκίνηση κορυφώθηκε με τη θέα του ολοκληρωμένου τετραέδρου του Sierpinski. Ήθελαν όλοι να το αγγίξουν, κάποιοι μάλιστα έχωσαν και το κεφάλι τους στο κούφιο εσωτερικό του. Ήταν ένα προϊόν δικό τους, μισό από το Α₂ και μισό από το Α₃. Πολλοί πρότειναν να το μεγαλώσουμε ακόμα περισσότερο, φτιάχνοντας άλλα τρία όμοιά του. Εμείς στρέψαμε την κουβέντα στα Μαθηματικά, επισφραγίζοντας την προσπάθεια με κάποιους γρίφους-σπαζοκεφαλιές. Οι απαντήσεις ήταν ολόσωστες ακόμα και στους πιο απαιτητικούς γρίφους. Έτσι βεβαιωθήκαμε ότι η μάθηση είχε επέλθει στους μαθητές μας.

Παρακάτω παραθέτουμε στοιχεία για την κατασκευή και τους γρίφους.

Οι καθηγητές
Ειρήνη Περυσινάκη, Αλέξανδρος Συγκελάκης

Σημεία ανάπτυξης

• Το τετράεδρο ως δομική μονάδα
• Το επαγωγικό χτίσιμο του τετραέδρου του Sierpinski
• Γρίφοι-σπαζοκεφαλιές
• Διαβάστε ακόμα

Για να χτίσουμε το τετράεδρο του Sierpinski χρειαζόμαστε πολλά, μικρά, τετράεδρα ως δομικούς λίθους. Μια πολύ απλή κατασκευή με τη μέθοδο της χαρτοδιπλωτικής (δηλαδή διπλώσεις χωρίς κόλλα) περιγράφεται στο ακόλουθο βίντεο:

Όπως φαίνεται, το τετράεδρο σχηματίζεται από μία μοναδική λουρίδα χαρτιού. Εμείς την λουρίδα την απλουστεύσαμε κατά πολύ, αφήνοντας ακριβώς εννέα ισόπλευρα τρίγωνα (παρακάτω εικόνα). Εδώ βρίσκεται ένα φυλλάδιο οδηγιών που ετοιμάσαμε: 3d_sierpinski_instructions.doc

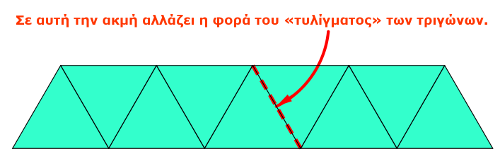
Με μια λουρίδα χαρτί κατασκεάζεται χωρίς κόλλα ένα τετράεδρο

Επιστροφή στα σημεία ανάπτυξης

Το τετράεδρο του Sierpinski είναι ένα fractal. Με απλά λόγια αυτό σημαίνει πως είναι το αποτέλεσμα μιας άπειρης διαδικασίας κατά την οποία παίρνουμε ένα αρχικό τετράεδρο και αρχίζουμε να «αδειάζουμε» το εσωτερικό του αφήνοντας μονάχα 4 τετράεδρα μισού μεγέθους στις κορυφές του και μετά πάλι κάνουμε το ίδιο για τα μικρότερα τετράεδρα κ.ο.κ. Το επόμενο βίντεο σκιαγραφεί με ωραίο τρόπο την άπειρη διαδικασία:

Στην πράξη, αυτό το άπειρο «άδειασμα» του τετραέδρου είναι αδύνατο. Αντιθέτως, μπορεί να πραγματοποιηθεί ένα «άπειρο» χτίσιμο με επαγωγικό τρόπο ως εξής: Με τέσσερα πανομοιότυπα τετράεδρα, ενωμένα στις κορυφές ανά δύο, κατασκευάζεται αρχικά ένα μεγαλύτερο τετράεδρο με «άδειο» εσωτερικό. Στην επόμενη φάση, με τέσερα από αυτά τα «κούφια» τετράεδρα, κατασκευάζεται, ακριβώς με τον ίδιο τρόπο, ένα ακόμα μεγαλύτερο τετράεδρο. Η διαδικασία αυτή θεωρητικά μπορεί να επαναληφθεί επ' άπειρον.

Το επαγωγικό χτίσιμο του τετραέδρου του Sierpinski

Επιστροφή στα σημεία ανάπτυξης

Ας πάρουμε ως μονάδα μήκους την ακμή του τετραέδρου-δομικού λίθου.

• Πόσα τετράεδρα-δομικούς λίθους έχει ένα τετράεδρο Sierpinski με ακμή 2 μονάδες, 4 μονάδες, 8 μονάδες, 16 μονάδες;
• Αν είχαμε ένα μυρμήγκι που περπατά επάνω στην επιφάνεια του τετραέδρου του Sierpinski, τότε σε πόσα ισόπλευρα τρίγωνα θα μπορούσε να περπατήσει συνολικά; Απαντήστε στις περιπτώσεις που το τετράεδρο του Sierpinski έχει ακμή 2 μονάδες, 4 μονάδες, 8 μονάδες, 16 μονάδες.
• Αν έχουμε δύο τετράεδρα Sierpinski, το ένα με διπλάσια ακμή από το άλλο, τότε ποια η σχέση των τετραέδρων-δομικών λίθων που έχει το καθένα;
• Ποιο πολύεδρο είναι το κενό που υπάρχει στο εσωτερικό ενός τετραέδρου Sierpinski με πλευρά 2 μονάδες; (ή αλλιώς, αν τεμαχίσουμε ένα τετράεδρο με επίπεδρα παράλληλα στις έδρες του που να διέρχονται από τα μέσα των ακμών του, τότε, ποια στερεά προκύπτουν ως τεμάχια;)

Επιστροφή στα σημεία ανάπτυξης

• Math Monday: Tetrahedron Ripples
• Sierpinski Tetrahedra and Other Fractal Sponges - The Geometry Jankyard

Επιστροφή στα σημεία ανάπτυξης