της Ειρήνης Περυσινάκη

Καθένας που έρχεται σε επαφή με το έργο του Αρχιμήδη δεν μπορεί παρά να θαυμάσει την μεγαλειώδη ιδιοφυΐα. Σκέψεις και μέθοδοι που ξεπέρασαν την εποχή του, που έθεσαν θεμέλια στην επιστήμη, που παρόμοιά τους συναντάμε μονάχα μετά από 2000 χρόνια. Αν τον είχαμε μπροστά μας, θα θέλαμε να μάθουμε το πώς συνέλαβε όλες αυτές τις ωραίες ιδές. Ευτυχώς, πρόλαβε την επιθυμία μας και άφησε κάποια κείμενα με τις "ευρετικές" του μεθόδους, δηλαδή τους συλλογισμούς που τον οδήγησαν στα θεωρήματά του, και οι οποίοι προηγούνται της αυστηρής μαθηματικής απόδειξης.

Το κυριότερο βιβλίο με ευρετικές μεθόδους είναι ή "Έφοδος" ή πιο σωστά το "Περί των μηχανικών θεωρημάτων προς Ερατοσθένην έφοδος". Εκείνο που θαυμάζουμε είναι οι τολμηρές ιδέες: Αντιμετωπίζει τα σχήματα σαν υλικά σώματα τα οποία κόβει, κολλάει, ζυγίζει. Κάτι τέτοιο θα δούμε στον "τετραγωνισμό ορθού κώνου τομής" (τετραγωνισμός παραβολής) που αναπτύσσεται παρακάτω (πλοηγηθείτε στις διαφάνειες με τα κουμπιά "αρχή", "προηγούμενο", "επόμενο", "τέλος").

αρχή       προηγούμενο       επόμενο       τέλος  "Καὶ γάρ τινα τῶν πρότερόν μοι φανέντων μηχανικῶς ὕστερον γεωμετρικῶς ἀπεδείχθη διὰ τὸ χωρὶς ἀποδείξεως εἶναι τὴν διὰ τούτου τοῦ τρόπου θεωρίαν∙ ἑτοιμότερον γάρ ἐστι προλαβόντα διὰ τοῦ τρόπου γνῶσίν τινα τῶν ζητημάτων πορίσασθαι τὴν ἀπόδειξιν μᾶλλον ἤ μηδενὸς ἐγνωσμένου ζητεῖν." Άλλωστε κάποιες ιδιότητες που στην αρχή μου αποκαλύφθηκαν με τη μηχανική στη συνέχεια αποδείχθηκαν με τη γεωμετρία, διότι η προσέγγιση που γίνεται με τη μέθοδο αυτή δεν επιδέχεται απόδειξης. Είναι ευκολότερο να οδηγηθείς στην απόδειξη, εάν έχεις αποκτήσει εκ των προτέρων κάποια γνώση του πράγματος, παρά αν ψάχνεις κάτι για το οποίο δεν έχεις την παραμικρή ιδέα. Αρχιμήδης, Περί των μηχανικών θεωρημάτων προς Ερατοσθένην έφοδος Αν κόψουμε έναν κώνο με ένα επίπεδο προκύπτουν διάφορες καμπύλες. Στην περίπτωση που το επίπεδο είναι παράλληλο προς μια γενέτειρα του κώνου (η ευθεία που διέρχεται από την κορυφή του κώνου και περιστρεφόμενη παράγει τον κώνο) η τομή είναι μια επίπεδη καμπύλη που καλείται παραβολή. Περιστρέψτε το τρισδιάστατο μοντέλο για να δείτε την παραβολή ως κωνική τομή. Η παραβολή είναι συμμετρική ως προς άξονα. Ο άξονας συμμετρίας της καλείται "διάμετρος". Το τμήμα που ενώνει δύο σημεία της παραβολής καλείται "χορδή". Δίπλα βλέπουμε την χορδή ΑΒ. Το χωρίο που περικλείεται από την παραβολή και μια χορδή της καλείται "παραβολικό τμήμα" και η χορδή καλείται "βάση" του παραβολικού τμήματος. Στον "τετραγωνισμό της παραβολής", ο Αρχιμήδης παίρνει ένα τυχαίο παραβολικό τμήμα με βάση ΑΒ και θεωρεί το εξής τρίγωνο: Πρώτα φέρνει από το Α παράλληλη προς την διάμετρο της παραβολής. Έπειτα φέρνει από το Β εφαπτομένη στην παραβολή΄που τέμνει την προηγούμενη ευθεία στο σημείο Γ. Έτσι ορίζεται το τρίγωνο ΑΒΓ. Αποδεικνύει ότι το εμβαδόν του παραβολικού τμήματος είναι το 1/3 του εμβαδού του τριγώνου ΑΒΓ. Στο εξής, θα συμβολίζουμε με παρένθεση το εμβαδόν, δηλαδή θα γράφουμε (ΑΒΓ). 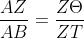Το πρώτο βήμα αποτελεί ο εντοπισμός της εξής "θεμελιώδους" ιδιότητας της παραβολής: Αν από τυχαίο σημείο Ζ της βάσης ΑΒ του τμήματος φέρουμε την παράλληλη προς την διάμετρο της παραβολής και είναι Θ το σημείο τομής της με την παραβολή και Τ το σημείο τομής της με την ΒΓ, τότε, Ας σημειώσουμε ότι για την απόδειξη αυτής της ιδιότητας, ο Αρχιμήδης χρησιμοποιεί την ομοιότητα τριγώνων και άλλες γνωστές σχέσεις που σήμερα θα λέγαμε ότι "η παραβολή έχει εξίσωση y=αx2". Αν τώρα πάρουμε δύο τραπέζια που έχουν ως βάση τους τα ΖΘ και ΖΤ και μη παράλληλες πλευρές που συγκλίνουν (όταν προεκταθούν) στο Β, τότε είναι εύκολο να αποδείξουμε ότι ο λόγος των εμβαδών τους είναι ο λόγος των βάσεών τους, δηλαδή: Συνεπώς, βάσει της θεμελιώδους ιδιότητας που αποδείχθηκε προηγουμένως, θα ισχύει: Και εδώ το ίδιο για τον ίδιο λόγο: Στη συνέχεια ακολουθούν ζυγίσεις, γι'αυτό ας θυμηθούμε μερικά στοιχειώδη σχετικά με αυτές: Αν ένα σώμα είναι κρεμασμένο από σχοινί και ηρεμεί, τότε ο φορέας του σχοινιού, που είναι κατακόρυφη ευθεία, διέρχεται από το κέντρο βάρους του σώματος. Στο διπλανό σχήμα εμφανίζεται ένας ζυγός ισορροπίας, όπου τα δύο βάρη είναι ίσα και οι αποστάσεις τους από το υπομόχλιο (τον κατακόρυφο άξονα) είναι επίσης ίσες. Τότε ο ζυγός ισορροπεί. Αν διπλασιαστεί η απόσταση του Β2 από το υπομόχλιο, τότε θα πρέπει να διπλασιάσουμε το βάρος Β1 προκειμένου ο ζυγός να εξακολουθεί να ισορροπεί. Αντίστοιχα, αν τριπλασιαστεί η απόσταση του Β2 από το υπομόχλιο, τότε θα πρέπει να τριπλασιάσουμε το βάρος Β1 προκειμένου ο ζυγός να εξακολουθεί να ισορροπεί. Γενικώς, τα βάρη στον ζυγό ισορροπίας και οι αποστάσεις τους από το υπομόχλιο είναι ποσά αντιστρόφως ανάλογα, δηλαδή 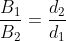Θα ζυγίσουμε τώρα το τρίγωνο ΑΒΓ, παίρνοντας φάλαγγα ζυγού το ΑΔ με ΔΑ=ΑΒ και υπομόχλιο το ΑΓ. Η ιδέα είναι να το διαιρέσουμε σε λουρίδες φέρνοντας κατακόρυφες ευθείες και να αντισταθμίσουμε κάθε λουρίδα με ένα ορθογώνιο. Ας εστιάσουμε την προσοχή μας σε μια από τις πολλές λουρίδες, που είναι ένα τραπέζιο ΕΖΤΣ. Αν τώρα σχεδιάσουμε και το τραπέζιο ΕΖΘΛ (Θ σημείο της παραβολής), τότε καθώς τα τραπέζια έχουν μη παράλληλες πλευρές που συγκλίνουν στο Β, θα ισχύει -όπως είπαμε προηγουμένως- η σχέση: Όμως ΑΒ=ΑΔ, οπότε η παραπάνω σχέση γίνεται: Συνεπώς, αν κρεμάσουμε το κόκκινο τραπέζιο (το ΕΖΘΛ) στο Δ και το γαλάζιο τραπέζιο (το ΕΖΤΣ) στο Ζ, αυτά θα ισορροπούν. Ναι, αλλά ήδη γνωρίζουμε ότι το γαλάζιο τραπέζιο ισορροπεί με ένα ορθογώνιο που επίσης κρέμεται από το Δ. Βέβαια, η απόσταση του γαλάζιου τραπεζίου από το υπομόχλιο σ' αυτήν την ζύγιση είναι μικρότερη από την προηγούμενη. Τα στοιχεία των δύο προηγούμενων διαφανειών, οδηγούν στο συμπέρασμα ότι το ορθογώνιο έχει μικρότερο εμβαδόν από το κόκκινο τραπέζιο. Αν αυτό γίνει συνολικά για όλες τις λουρίδες, συμπεραίνουμε ότι στο σύνολό τους όλα τα ορθογώνια που αντισταθμίζουν το τρίγωνο είναι μια επιφάνεια (θα την ονομάσουμε Χ) μικρότερη από ένα σύνολο τραπεζίων που καλύπτουν το παραβολικό τμήμα. Ανάλογα αποδεικνύεται ότι η επιφάνεια Χ είναι μεγαλύτερη από ένα σύνολο τραπεζίων στο εσωτερικό του παραβολικού τμήματος. Σχηματικά έχουμε ένα πάνω φράγμα και ένα κάτω φράγμα για το εμβαδόν της άγνωστης επιφάνειας Χ. Το μεν άνω φράγμα υπερβαίνει το εμβαδόν του παραβολικού τμήματος (το ονομάζουμε Π1), το δε κάτω φράγμα (που ονομάζουμε Π2) είναι μικρότερο από το εμβαδόν του παραβολικού τμήματος. Υποψιαζόμαστε πως το (Χ) θα πρέπει να είναι ίσο με το εμβαδόν του παραβολικού τμήματος. Αρκεί να δείξουμε ότι η διαφορά (Π1)-(Π2) μπορεί να γίνει οσοδήποτε μικρή θελήσουμε. Πραγματικά, η διαφορά (Π1)-(Π2) μπορεί να γίνει οσοδήποτε μικρή θελήσουμε. Εδώ θα εκθέσουμε ένα επιχείρημα όπου η διαφορά γίνεται ακριβώς ίση με το 1/5 του (ΑΒΓ). Διαρούμε το ΑΓ σε 5 ίσα τμήματα, ένα εξ αυτών το ΑΔ. Τότε, (ΑΒΔ) = (ΑΒΓ)/5 Φέρνουμε κατακόρυφες ευθείες (παράλληλες στη διάμετρο της παραβολής) που διέρχονται από τα σημεία τομής των πλαγίων τμημάτων και της παραβολής. Παρακολουθήστε τώρα αυτά τα τραπέζια και τα ισεμβαδικά τους που θα εμφανιστούν στις επόμενες διαφάνειες. Αυτό το νέο κόκκινο τραπέζιο που εμφανίστηκε, έχει εμβαδόν ίσο με το προηγούμενο κόκκινο τραπέζιο που εξαφανίστηκε. Ομοίως, αυτό το νέο πράσινο τραπέζιο που εμφανίστηκε, έχει εμβαδόν ίσο με το προηγούμενο πράσινο τραπέζιο που εξαφανίστηκε. Όμοια και εδώ. Ολοκληρώνοντας την διαδικασία παρατηρούμε ότι τα έγχρωμα μέρη συνθέτουν ακριβώς την διαφορά (Π1)-(Π2). Συνεπώς, Εφόσον η διαφορά (Π1)-(Π2) μπορεί να γίνει οσοδήποτε μικρή θελήσουμε, συμπεραίνουμε ότι στην ζύγιση που κάναμε, η άγνωστη επιφάνεια Χ που αντισταθμίζει το τρίγωνο ΑΒΓ έχει εμβαδόν ίσο με το εμβαδόν του παραβολικού τμήματος. Ας κρεμάσουμε τώρα το τρίγωνο ΑΒΓ από το σημείο Ε, από όπου η κατακόρυφη ευθεία "συναντά" το κέντρο βάρους G του τριγώνου ΑΒΓ. Το τρίγωνο θα βρίσκεται σε ηρεμία στην ίδια θέση όπως πριν, οπότε ο ζυγός και πάλι θα ισορροπεί. 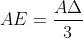Όμως, είναι γνωστό πως ΑΕ = ΑΒ/3 και επειδή ΑΒ = ΑΔ, θα έχουμε ότι Και λόγω ισορροπίας Συνδυάζοντας τα παραπάνω παίρνουμε ότι που είναι και το ζητούμενο. Κλείνουμε με την σημερινή προσέγγιση του εμβαδού του παραβολικού τμήμτος. Είναι τα λεγόμενα "κάτω" και "πάνω" αθροίσματα, τα θεμέλια του "ολοκληρώματος". Τι άλλαξε; Ίσως όχι και πολλά... Αντί για τραπέζια, έχουμε ορθογώνια!

Ευάγγελος Σταμάτης «Επιστημονικαί εργασίαι – άρθρα», Τόμος Α', 1972, σελ. 35-81
http://evangelosstamatis.wordpress.com/bibliography/

Η παραπάνω παρουσίαση πραγματοποιήθηκε στις 13 Μαρτίου 2013, στην ημερίδα του Πρότυπου Πειραματικού Γυμνασίου με θέμα "Σύγχρονα θέματα από την Αρχαία Ελληνική Επιστήμη" (περίληψη της παρουσίασης).

Η ημερίδα αυτή ήταν μία από τις πολλές εκδηλώσεις που πλαισίωσαν την έκθεση της "Αρχαίας Ελληνικής Τεχνολογίας" του κ. Κώστα Κοτσανά (ιστότοπος έκθεσης).