Διαβάστε το άρθρο σε pdf

Η συνταγή για ένα επιτυχημένο μαγικό συνίσταται στο ότι

• ο μάγος πρέπει να γνωρίζει κάτι που δε γνωρίζουν οι θεατές
• κάποια «κρίσιμα» βήματα του τρυκ πρέπει να μην εκτεθούν σε κοινή θέα

Αυτό που στην περίπτωση μας γνωρίζει ο γεωμέτρης μάγος, που ευελπιστεί ότι δεν το γνωρίζουν ή έστω δεν το φαντάζονται αυτοί στους οποίους απευθύνεται, είναι ένας γεωμετρικός τόπος που σχετίζεται με ένα γεωμετρικό μετασχηματισμό. Ο μετασχηματισμός είναι αυτός της στροφής. Ο γεωμετρικός τόπος ακολουθεί.

Έστω δοσμένη ευθεία (ε) και ένα σταθερό σημείο Κ εκτός αυτής. Οι ημιευθείες Κx και Κy σχηματίζουν την κυρτή γωνία ∠xΚy σταθερού μέτρου φ. Η γωνία αυτή στρέφεται με κέντρο το Κ και έστω Α το εκάστοτε σημείο τομής της (ε) με την Kx. Να βρεθεί ο γεωμετρικός τόπος των σημείων Β επί της Κy για τα οποία ΚΒ=ΚΑ.

Ας βρούμε τον εν λόγω γεωμετρικό τόπο.

Από το σημείο Κ φέρουμε την κάθετο επί της (ε). Η εν λόγω κάθετος και η (ε) τέμνονται στο σημείο Μ. Σχηματίζουμε το ισοσκελές τρίγωνο ΛΚΝ (ΚΛ=ΚΝ) έτσι ώστε το μέτρο της γωνίας ∠ΛΚN να είναι φ. Είναι προφανές ότι το μέτρο της ∠ΜΚΝ είναι φ/2 και το Ν είναι ένα σταθερό σημείο επί της (ε) το οποίο ανήκει στο γεωμετρικό τόπο. Φέρουμε την μπλε χρώματος ευθεία που διέρχεται από το Ν και σχηματίζει γωνία φ με την (ε), όπως ακριβώς φαίνεται στο σχήμα.

Δείτε το «μαγικό» σε δυναμικό σχήμα

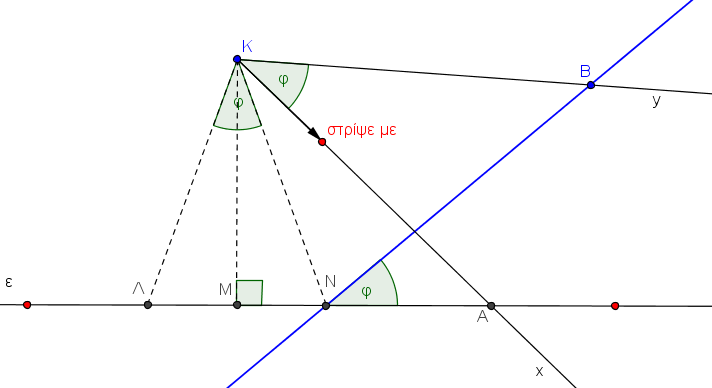
Θα δείξουμε ότι όλα τα σημεία της μπλε γραμμής ικανοποιούν τη συνθήκη του ζητούμενου γεωμετρικού τόπου. Έστω η τυχαία μη χαρακτηριστική θέση της γωνίας ∠xKy που φαίνεται στο σχήμα. Αρκεί να δείξουμε ότι ΚΑ=ΚΒ. Έχει γίνει πλέον εμφανές ότι θα πρέπει να δείξουμε ότι τα τρίγωνα ΛΚΑ και ΝΚΒ είναι ίσα. Έχουμε ΚΛ=ΚΝ, ∠ΛΚΑ=φ+∠ΝΚΑ=∠ΝΚΒ και ∠ΚΛΑ=1^L-φ/2 και επίσης ∠ΚΝΒ=2^L-(1^L-φ/2)-φ=1^L-φ /2, δηλαδή ∠ΚΛΑ=∠ΚΜΒ και πράγματι τα τρίγωνα ΛΚΑ και ΜΚΒ είναι ίσα. Η ισότητα αυτή των τριγώνων μάς οδηγεί στο προς απόδειξη ΚΑ=ΚΒ.

Στη συνέχεια εύκολα με τη βοήθεια της εις άτοπον απαγωγής μπορούμε να δείξουμε ότι δεν υπάρχουν σημεία Β που να βρίσκονται εκτός της μπλε γραμμής η οποία μετά από όλα αυτά είναι ο ζητούμενος γεωμετρικός τόπος.

Με τη βοήθεια των παραπάνω μπορούμε άμεσα να κάνουμε την ακόλουθη κατασκευή:

Έστω ορθογώνιο τρίγωνο ΑΒΓ (∠Α=1^L) και ακόμη έστω ένα σταθερό σημείο Κ επί της πλευράς ΑΒ του εν λόγω τριγώνου. Να κατασκευασθεί ισόπλευρο τρίγωνο εγγεγραμμένο στο ΑΒΓ του οποίου η μια κορυφή να είναι το σημείο Κ.

Λύση

Δείτε την κατασκευή βήμα-βήμα σε δυναμικό σχήμα

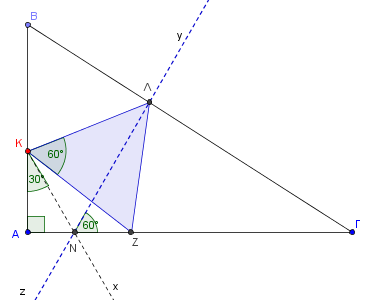
Έστω ΚΛΖ το εγγεγραμμένο ισόπλευρο τρίγωνο.

Έχουμε ΚΛ=ΚΖ και ∠ΖΚΛ=60^ο με το Ζ να κείται επί της ΑΓ. Σύμφωνα με τα προηγούμενα το Λ θα είναι ένα σημείο της μπλε ευθείας η οποία προκύπτει ως εξής: Κατασκευάζουμε την ημιευθεία Κx έτσι ώστε ∠ΑΚx=30^ο και έτσι προκύπτει το σημείο Ν. H μπλε ευθεία είναι η ευθεία zy που διέρχεται από το Ν και σχηματίζει γωνία ∠yΝΓ=60^ο. Το σημείο Λ είναι το σημείο τομής της ΒΓ με την zy. Αν και μένουν ακόμα κάποια «διαδικαστικά», η κατασκευή είναι προφανής.

Και τώρα το τρυκ

Δίνουμε κατευθείαν προς λύση το παραπάνω πρόβλημα χωρίς να αναφερθούμε καθόλου στα προηγηθέντα βήματα που εμείς ασφαλώς γνωρίζουμε και θα τα έχουμε στο μυαλό μας για να λύσουμε το πρόβλημα «ανεξάρτητα» και με τρόπο «μαγικό»

Ας προχωρήσουμε

Δείτε την κατασκευή βήμα-βήμα σε δυναμικό σχήμα

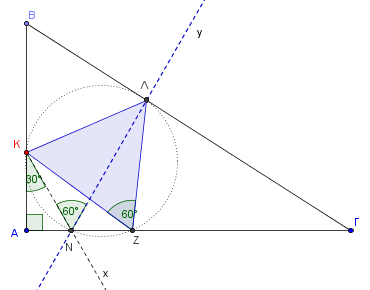
Έστω ΚΛΖ το εγγεγραμμένο ισόπλευρο τρίγωνο.

Αν προσδιορίσουμε το σημείο Λ το πρόβλημα μας ουσιαστικά έχει λυθεί.

Έστω το ευθύγραμμο τμήμα ΛΝ έτσι ώστε ∠ΛΝΓ=60^ο. Φέρουμε και το ευθύγραμμο τμήμα ΚΝ. Επειδή ∠ΛΝΓ=∠ΖΚΛ=60^ο το τετράπλευρο ΚΝΖΛ είναι εγγράψιμο σε κύκλο και κατά συνέπεια ∠ΚΝΑ=∠ΚΛΖ=60^ο⇒∠ΑΚΝ=30^ο.

Δηλαδή το σημείο Λ προκύπτει ως ακολούθως:

Κατασκευάζουμε την ημιευθεία Κx έτσι ώστε ∠ΑΚx=30^ο και με αυτόν τον τρόπο προσδιορίζουμε το σημείο τομής Ν της παραπάνω ημιευθείας με το ευθύγραμμο τμήμα ΑΓ.

Το σημείο τομής της ημιευθείας Νy με το ευθύγραμμο τμήμα ΒΓ είναι το ζητούμενο σημείο Λ.

Για να έχει το πρόβλημα λύση θα πρέπει το σημείο Ν να είναι σημείο του ευθύγραμμου τμήματος ΑΓ.

Εναλλακτικά αντί του Λ με εντελώς ανάλογο τρόπο θα μπορούσαμε να προσδιορίσουμε το σημείο Ζ.

Τελειώνοντας θα 'θελα να ζητήσω συγγνώμη από το Μέγα Ευκλείδη, γιατί κάποια πράγματα- που εδώ δεν αναφέρω - τα έκλεισα σε έναν υποθετικό φάκελο που γράφει απέξω «Διαδικαστικά».

Ε. Λαμπράκης